更新:2024-02-18 22:31:02精品经验
用Mathematica来演示一下,椭圆{5 Cos[t] ,3 Sin[t]}在复平面上进行复变换之后的图形。
工具/原料
电脑Mathematica方法/步骤
1/8分步阅读给定复数z = 5 Cos[t] + 3 I Sin[t],当t取不同的值,z在复平面上的图形是一个椭圆,椭圆的参数方程,恰好就是复数z的实部和虚部——ReIm[z] :
ParametricPlot[ReIm[z], {t, 0, 2 Pi}, PlotLabel -> z]
 [图]2/8
[图]2/8对z进行平方运算,看看能得到一条什么曲线:
a0 = z^2;
ParametricPlot[{ReIm[z], ReIm[a0]}, {t, 0, 2 Pi}, PlotLabel -> {z, a0}]
注意看,图中的蓝色线就是z对应的椭圆,黄色线就是z^2的图像。
 [图]3/8
[图]3/8如果对z进行开平方呢?
a00 = z^(1/2);
ParametricPlot[{ReIm[z], ReIm[a00]}, {t, 0, 2 Pi}, PlotLabel -> {z, a00}]
 [图]4/8
[图]4/8开平方运算,让图形看起来 "少了一半"。用一个动图来展示一下这个图形的作图过程:
Manipulate[
ParametricPlot[{ReIm[z], ReIm[an]}, {t, 0, tt},
PlotRange -> {{-5, 5}, {-3, 3}},
PlotLabel -> {z, an}], {tt, 0.001, 2 Pi}]
 [图]5/8
[图]5/8用动图展示一下z^n,n从0到2之间,图形的变换情况:
Manipulate[
ParametricPlot[{ReIm[z], ReIm[z^n]}, {t, 0, 2 Pi},
PlotRange -> {{-10, 25}, {-15, 15}}, PlotLabel -> {z, z^n}], {n, 0, 2}]
 [图]6/8
[图]6/8如果对z进行正弦变换,图形如下:
b = Sin[z];
ParametricPlot[{ReIm[z], ReIm[b]}, {t, 0, 2 Pi},PlotLabel -> {z, b}]
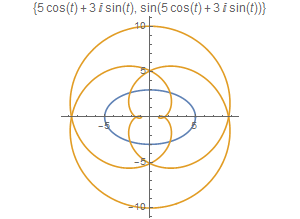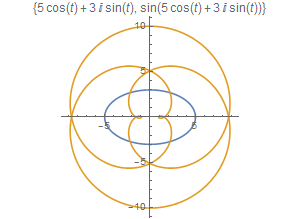 [图]7/8
[图]7/8Sin[z]的图像的作图过程:
b0 = Sin[z];
Manipulate[
ParametricPlot[{ReIm[z], ReIm[b0]}, {t, 0, tt},
PlotRange -> {{-9, 9}, {-10, 10}}, PlotLabel -> {z, b0}], {tt, 0.001, 2 Pi}]
 [图]8/8
[图]8/8再来看看Sin[z^n],n从0到1.2之间变化,对应的图形:
Manipulate[
ParametricPlot[{ReIm[z], ReIm[Sin[z^n]]}, {t, 0, tt},
PlotRange -> {{-18, 26}, {-24, 24}},
PlotLabel -> {z, Sin[z^n]}], {tt, 0.001, 2 Pi}, {n, 0, 1.2}]
 [图]
[图]情感/交际经验推荐
- Q[视频]苹果手机怎么设置指纹解锁
- Q你知道如何写情侣甜蜜恩爱语写
- Q请告诉下情侣之间如何相处才能长久
- Q专栏如何让一个内向的人变外向 变得越来越...
- Q优秀怎样布置两人生日浪漫房间
- Q什么情况女人一旦对男人动了真情会有什么样的表...
- Q听说女人微信回复一个“嗯”字是什么意思?
- Q有办法怎么追自己喜欢的人
- Q求问如何免费开网店详细步骤 新手篇
- Q头条男人怎样做,女人才能越来越喜欢你?
- Q这种如何提高你的沟通技巧
- Q怎么做男人怎样做,女人才能越来越喜欢你?
- Q哪儿单删微信好友再加回来他有消息提示吗
- Q头条怎样让自己变得有气质
- Q精选闺蜜生日送什么礼物合适?
- Q有知道女朋友(女生)生理期肚子疼怎么办?
- Q有没有怎么知道男人喜欢你?
- Q专栏读心术?教你如何看透一个人
- Q什么情况教你怎么还人情
- Q求推荐如何委婉拒绝别人的邀约
- Q[视频]如果抖音怎么把人拉黑并取消黑名单
- QWin10如何使用背景聚焦功能
- Q[视频]霓虹深渊无限纪念品怎么获得
- Q[视频]怎么学触发器ppt怎么弄的
已有 31665 位经验达人注册
已帮助 142691 人解决了问题


