[视频]【抽象代数】不同的域里面的因式分解
关于天地劫【抽象代数】不同的域里面的因式分解,期待您的经验分享,感谢你,我会记得你对我的好的
!
更新:2024-03-31 15:08:43优秀经验
来自马蜂窝https://www.mafengwo.cn/的优秀用户无情天魔精致,于2018-12-19在生活百科知识平台总结分享了一篇关于“【抽象代数】不同的域里面的因式分解张朝阳”的经验,非常感谢无情天魔精致的辛苦付出,他总结的解决技巧方法及常用办法如下:
 [图]2/6
[图]2/6 [图]3/6
[图]3/6 [图]4/6
[图]4/6 [图]5/6
[图]5/6 [图]6/6
[图]6/6 [图]
[图]
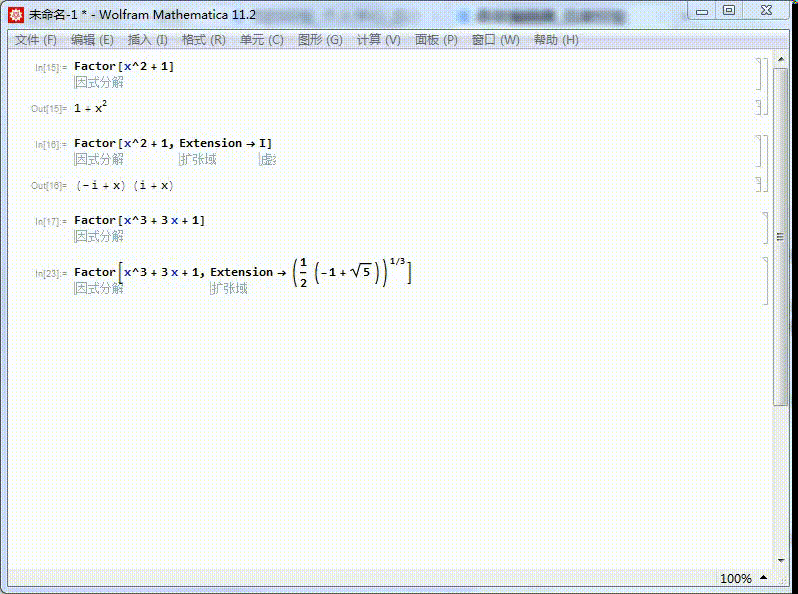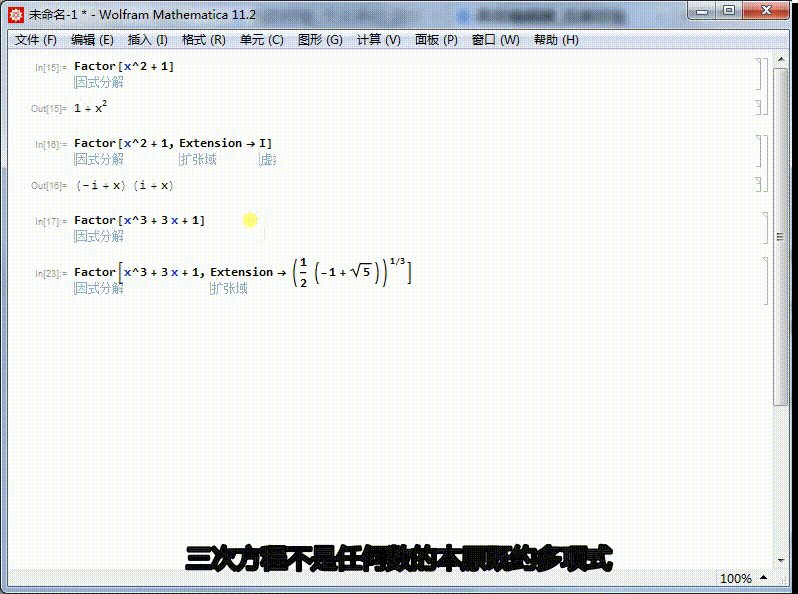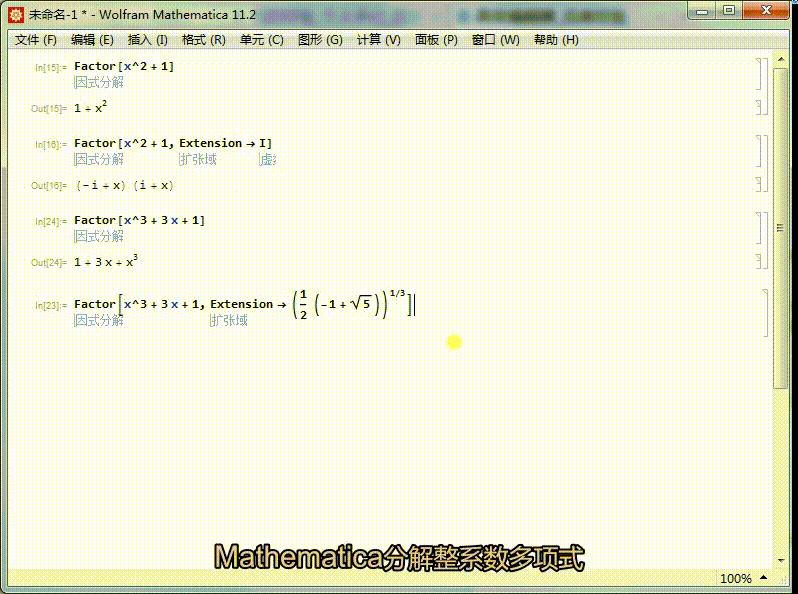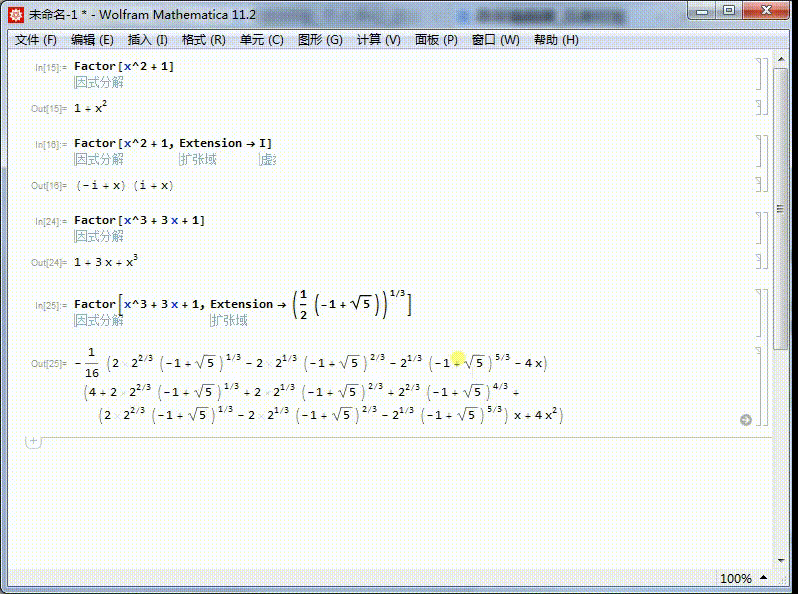
在实数域里面,x^2+1是不能分解的,因此可以认为它是虚数单位i的本原既约多项式。当然,这个说法必须指出是在实数域里面成立。在复数域,i的本原既约多项式是x-i。
工具/原料
电脑mathematica方法/步骤
1/6分步阅读x^3+3x+1=0
任意三次方程必有一个实根。因此,在实数域内,三次方程不是任何数的本原既约多项式。
但是为什么Mathematica不能分解它呢?这是因为,Mathematica分解整系数多项式,默认的是整数范围内。
如果我们使用某种扩域,就会好得多。
 [图]2/6
[图]2/6在素域F2里面,x^2+1可以分解为(x+1)^2,因为2x=0x=0。
.
 [图]3/6
[图]3/6在素域F5里面,x^2+1可以分解为(x+2)(x+3)。
 [图]4/6
[图]4/6在素域F3里面,x^2+1不能分解。
 [图]5/6
[图]5/6看一下,x^7+1在不同的域里面的分解情况。
.
你会发现,在不同的素域里面,分解情况竟然是截然不同的。
 [图]6/6
[图]6/6同样的,x^3+3x+1在不同的域里面,也有不同的分解。
 [图]
[图]编辑于2018-12-19,内容仅供参考并受版权保护
经验备注
我发现了这篇经验很有用:你也认同《【抽象代数】不同的域里面的因式分解》的经验分享有价值,就请和朋友们一起分享吧。另外,【抽象代数】不同的域里面的因式分解的经验内容仅供参考,如果您需解决具体问题(尤其法律、医学等领域),建议您详细咨询相关领域专业人士。经验知识实用生活指南-解决你所有的生活难题!未经许可,谢绝转载。本文网址:https://www.5058.cn/article/8275fc862dfcde46a03cf68a.html
时尚/美容经验推荐
- Q[视频]快手个人介绍怎么写
- Q什么样的怎样瘦腿才是最快方法
- Q怎么做朋友圈一条线是屏蔽了还是删除了
- Q有晓得学生瘦脸的最快方法
- Q告诉如何瘦肚子:怎样快速瘦肚子
- Q怎么看瑜伽入门动作图片教程
- Q回答下怎样让脸变白
- Q要怎么领带打结详解
- Q那里正确的淡妆化妆步骤-怎样画淡妆
- Q为何淑女怎样扎出小清新发型
- Q告诉中国护肤品十大品牌排行榜
- Q哪里全球护肤品十大排名,买得起的大牌必须...
- Q知道中学生怎样快速瘦腿
- Q学习中国护肤品十大品牌排行榜
- Q那么牛仔阔腿裤搭配什么鞋
- Q推荐夏天穿内衣很热怎么办
- Q什么全球十大护肤品排行榜,十款性价比高的...
- Q介绍怎样快速瘦肚子
- Q这里怎么瘦大腿和屁股
- Q问大家中学生怎样快速瘦腿
- Q王者荣耀如何进行巅峰赛
- Q[视频]想知道@163.com这个邮箱该怎么登录?
- Q王者荣耀如何获得战令经验
- Q12368如何转人工?
已有 51279 位经验达人注册
已帮助 152979 人解决了问题


