[视频]【Mathematica】寻找可截断的素数

方法/步骤

代码截图如下。

这是一个自定义函数TruncatablePrimes，其变量是正整数p，如果p不是素数，则返回一个空列表，如果p是素数，就新建一个包含p的子列表，并在这个子列表里面重复调用TruncatablePrimes函数，不过呢，此时TruncatablePrimes的变量，变成了在p的左边添加一个1到9的数字而形成的新的数字。

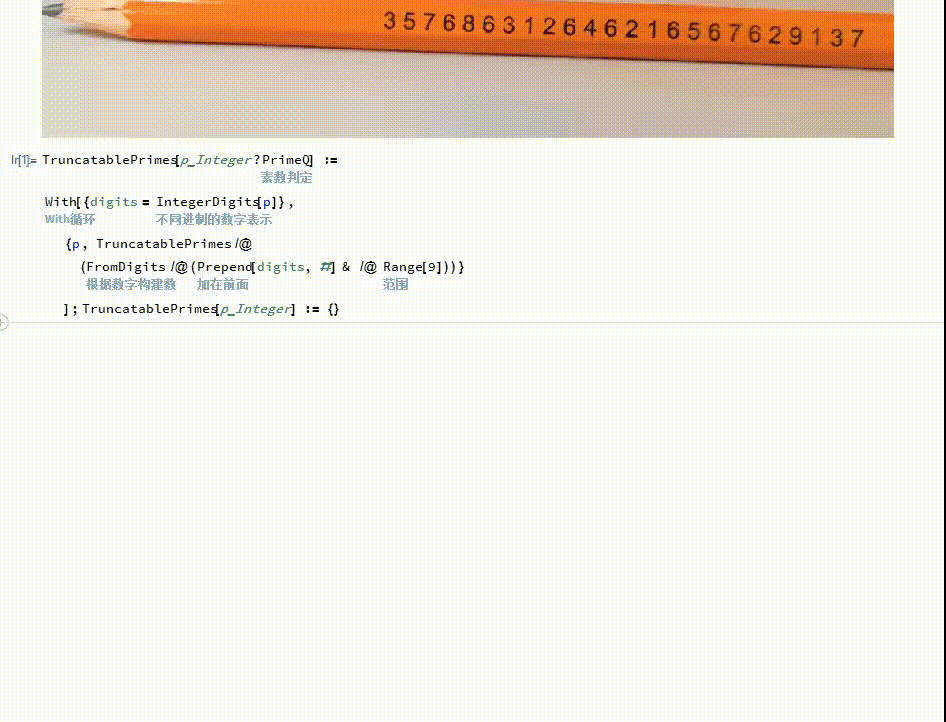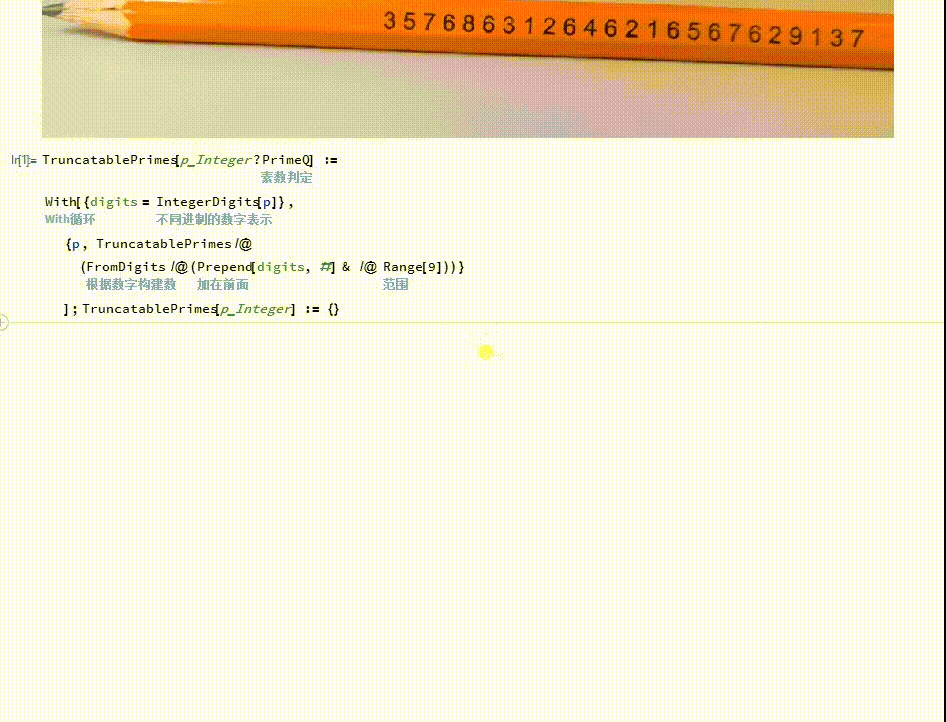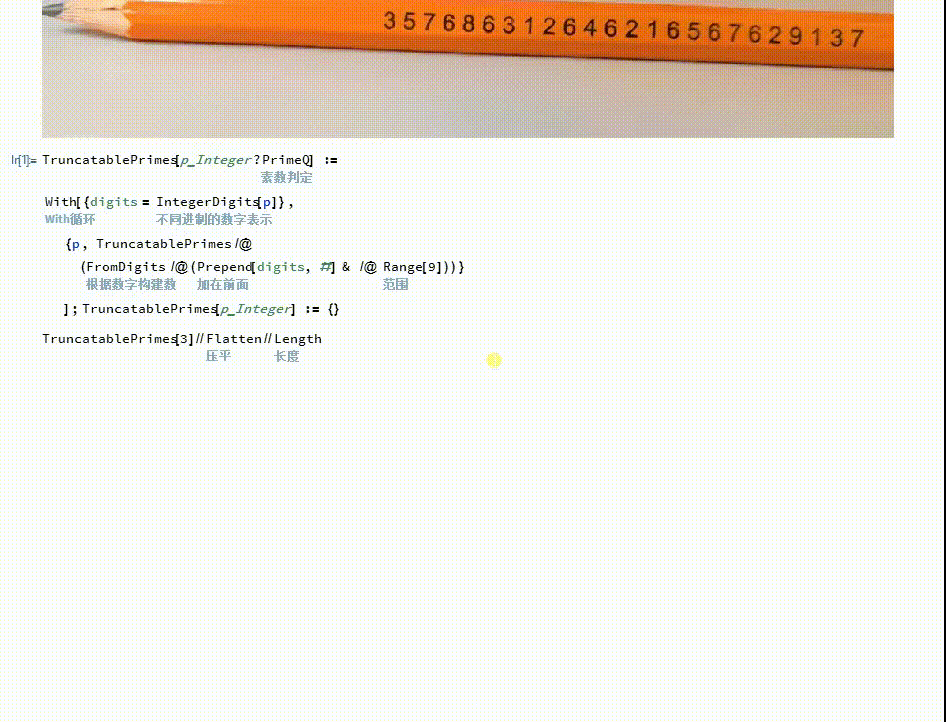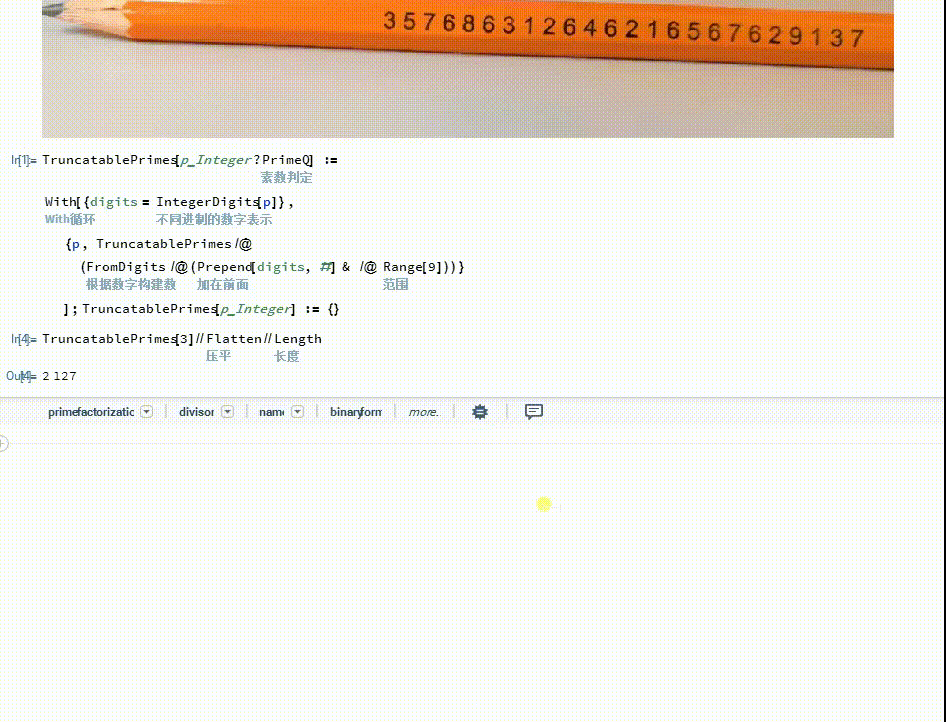
以数字3结尾的截断素数，一共有2127个。

TruncatablePrimes[3]//Flatten//Length

以数字3结尾的最大截断素数是：

Max[TruncatablePrimes[3]//Flatten]

以数字1结尾的截断素数，需要分成五大类来寻找：

Column[Max[TruncatablePrimes[#]//Flatten]&/@{11,31,41,61,71}]

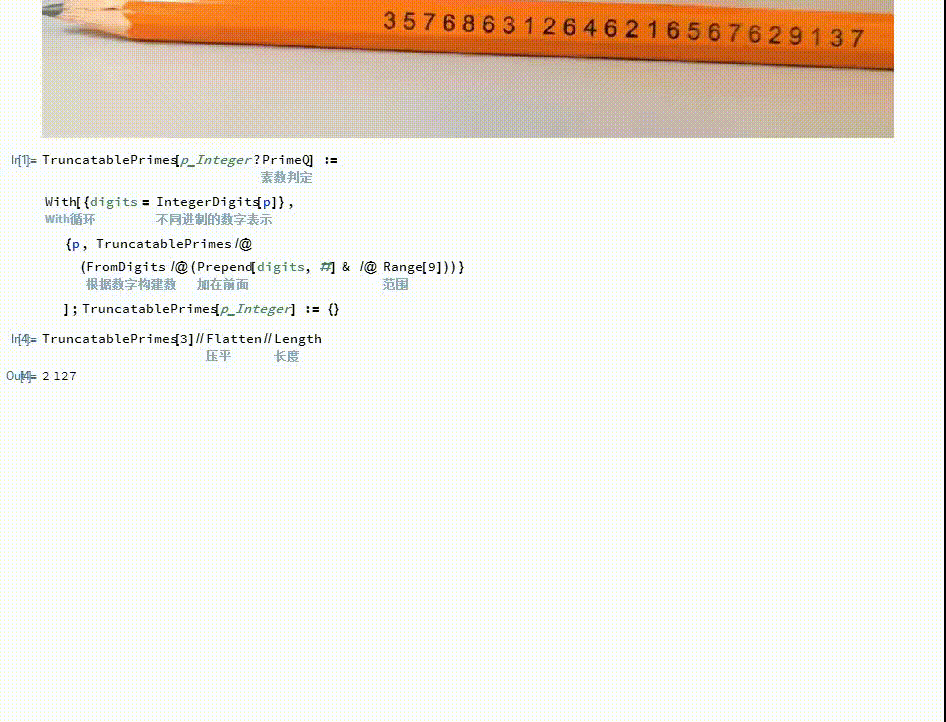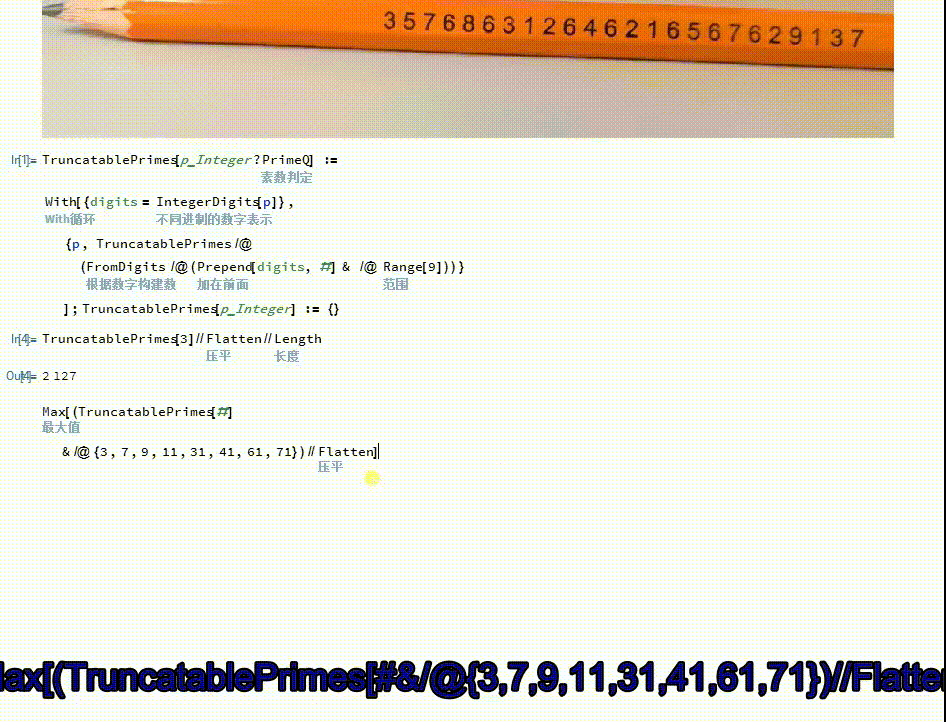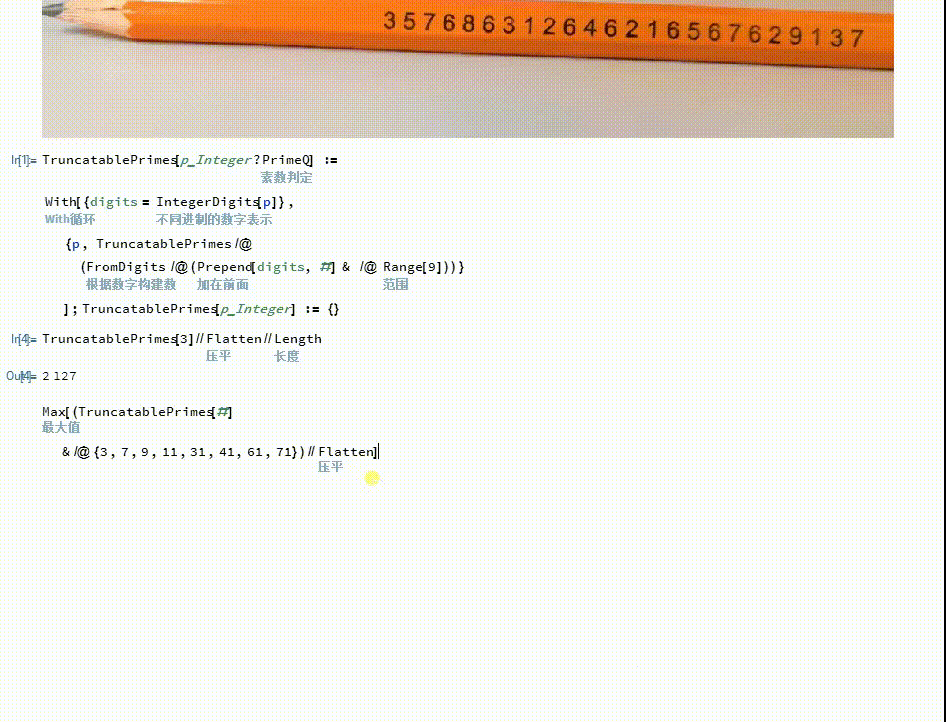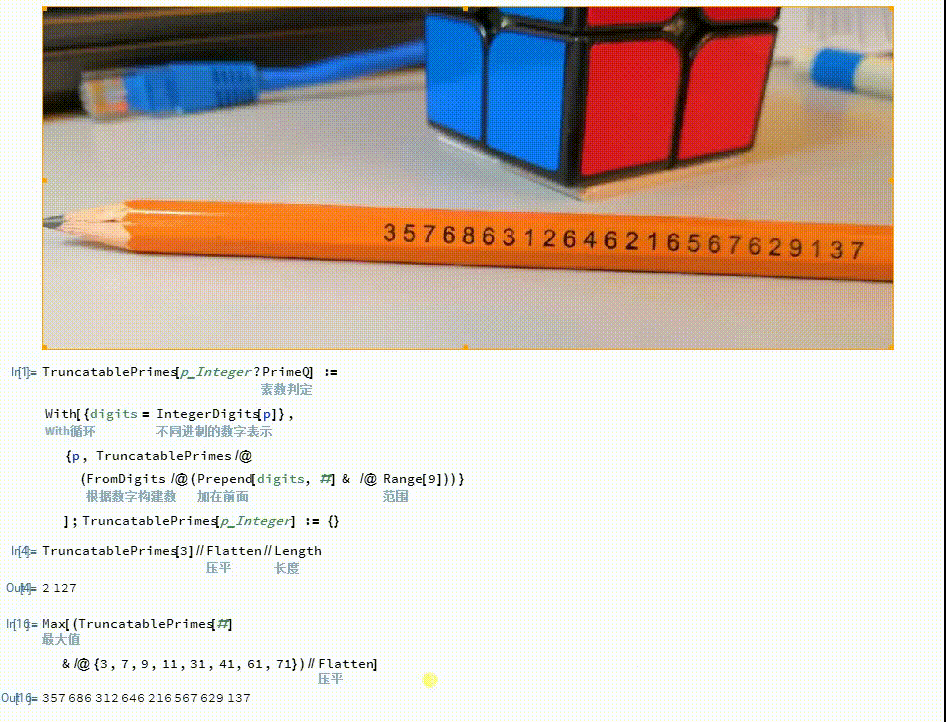
通过枚举法可以证明，作者铅笔上的素数是最大的截断素数。

Max[(TruncatablePrimes[#&/@{3,7,9,11,31,41,61,71})//Flatten]

不过，作者在原文给出的寻找最大的截断素数的代码是有疏漏的：

Take[Sort[Flatten[TruncatablePrime/@ Range[9]]], -5]

因为1默认不是素数，所以把1作为TruncatablePrime的变量，将返回一个空列表。这样导致的后果是，在枚举截断素数的时候，以1结尾的截断素数被忽略了。

编辑于2018-12-30，内容仅供参考并受版权保护

经验备注

本文网址：https://www.5058.cn/article/d5a880ebfb88c113f147ccab.html