[视频]【Mathematica】构造一般多项式
关于雪纳瑞【Mathematica】构造一般多项式,期待您的经验分享,你无异于雪中送炭,让我感激涕零
!
更新:2024-02-28 22:40:18头条经验
来自百度https://www.baidu.com/的优秀用户无情天魔精致,于2018-12-16在生活百科知识平台总结分享了一篇关于“【Mathematica】构造一般多项式俯卧撑”的经验,非常感谢无情天魔精致的辛苦付出,他总结的解决技巧方法及常用办法如下:
 [图]2/6
[图]2/6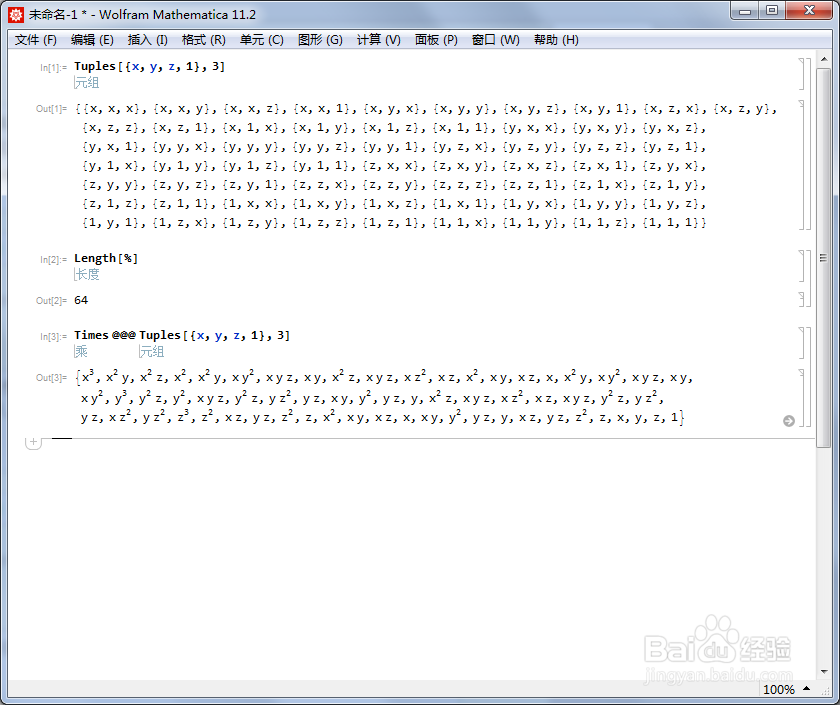 [图]3/6
[图]3/6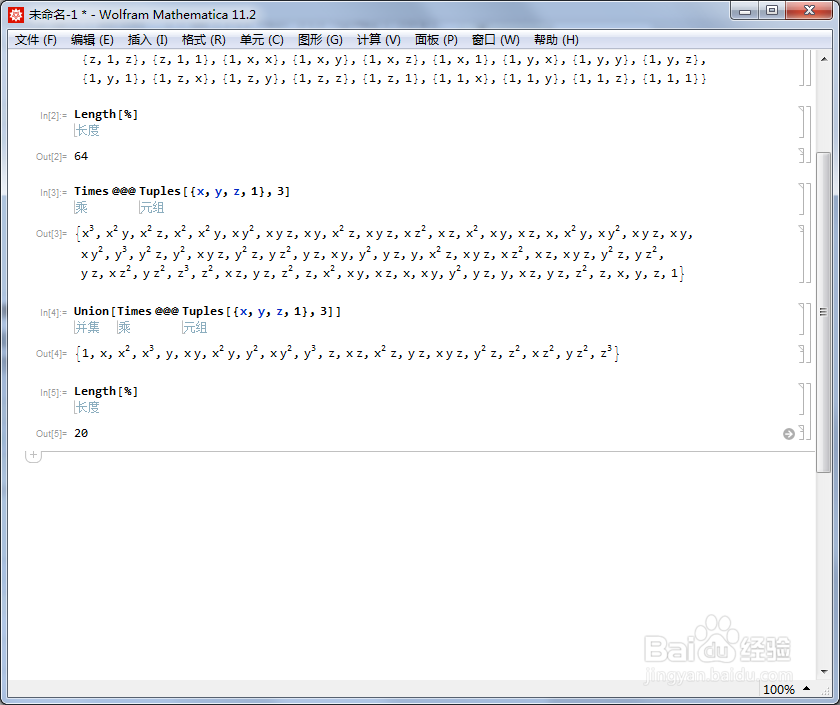 [图]4/6
[图]4/6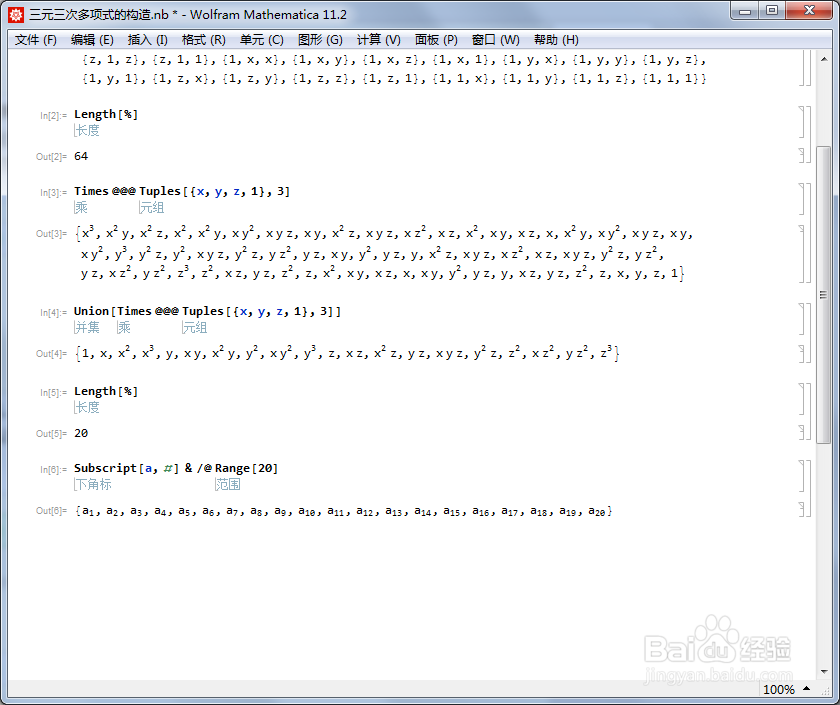 [图]5/6
[图]5/6 [图]6/6
[图]6/6 [图]
[图]
本文,用Mathematica来构造一般多项式。如果变量是x、y、z,最高次数是3,就表示这是一个三元三次多项式。下面,我们就以三元三次多项式为例,来加以介绍。
工具/原料
电脑Mathematica方法/步骤
1/6分步阅读每次从列表{x,y,z,1}里面拿出一个元素,拿三次,会有多少种情况呢?
这一点,我们可以通过Tuples实现,而且得到答案是64种。
这是对的,因为4的4次方就是64。
 [图]2/6
[图]2/6每一种情形的三个元素相乘,就得到一个次数不大于3的、关于x,y,z的单项式,其中包括常数项,用1表示,代表了x,y,z的指数都是0。
 [图]3/6
[图]3/6不过这里面有重复项,需要合并起来,这类似于单项式的合并同类项。
这一点,可以通过Union实现。
合并之后,只剩下20项,这恰好是三元三次多项式所需要的全部项。
 [图]4/6
[图]4/6给出各项的系数。
我们准备用a1,a2,……,a20来作为系数。
 [图]5/6
[图]5/6系数的集合,可以视为20维的向量;
单项式的集合,也可以视为20为向量;
这两个向量的点积,就是一个三元三次多项式。
 [图]6/6
[图]6/6整合一下,可以写出一个命令Sydxs,用来构造三元多项式。
应用这个命令,可以构造一个一般的三元四次多项式,并发现它有35项。
 [图]
[图]编辑于2018-12-16,内容仅供参考并受版权保护
经验备注
我发现了这篇经验很有用:你也认同《【Mathematica】构造一般多项式》的经验分享有价值,就请和朋友们一起分享吧。另外,【Mathematica】构造一般多项式的经验内容仅供参考,如果您需解决具体问题(尤其法律、医学等领域),建议您详细咨询相关领域专业人士。经验知识实用生活指南-解决你所有的生活难题!未经许可,谢绝转载。本文网址:https://www.5058.cn/article/3065b3b6467068becff8a49f.html
职场/理财经验推荐
- Q小米定时开关机
- Q头条上海企业人力资源管理师四级怎么申请补...
- Q谁知道2021淘宝开店流程及费用,淘宝开店需要...
- Q听说淘宝店铺装修教程2021新版,10分钟学会...
- Q哪个通过住房和城乡建设部政务服务门户加注...
- Q如何中国银行怎么拨打人工服务
- Q免费怎样炒股——股市新手入门口诀!
- Q推荐k线图基础知识k线基本形态分析
- Q阐述新手该如何操作国债逆回购?有什么流程...
- Q了解下双色球开奖号码怎么算中奖
- Q问一下查询自己名下证券账户
- Q是什么新手如何开淘宝店
- Q请告诉下手机号不用了怎么办?移动手机卡如何办...
- Q那些个体营业执照怎么注销可以网上办理
- Q如何选择新手怎样开网店详细步骤,1天学会开网...
- Q有了解2019最新工资个人所得税税率表
- Q这个手把手教你开网店
- Q怎么做税控盘注销操作流程
- Q那么如何通过EXCEL统计表格里面的符号
- Q[视频]凉拌银耳的家常做法
- Q如何开启手机微信步数
- Q超级人类登录发生延迟怎么办?
- Q抖音如何彻底清除观看历史
已有 59035 位经验达人注册
已帮助 235499 人解决了问题


