[视频]【抽象代数】用Mathematica判定代数整数
关于修真聊天群【抽象代数】用Mathematica判定代数整数,期待您的经验分享,谢了,下次有事儿别忘了找我
!
更新:2024-02-25 19:23:09杰出经验
来自凤凰网https://www.ifeng.com/的优秀用户无情天魔精致,于2018-12-01在生活百科知识平台总结分享了一篇关于“【抽象代数】用Mathematica判定代数整数我的英雄学院”的经验,非常感谢无情天魔精致的辛苦付出,他总结的解决技巧方法及常用办法如下:
 [图]2/6
[图]2/6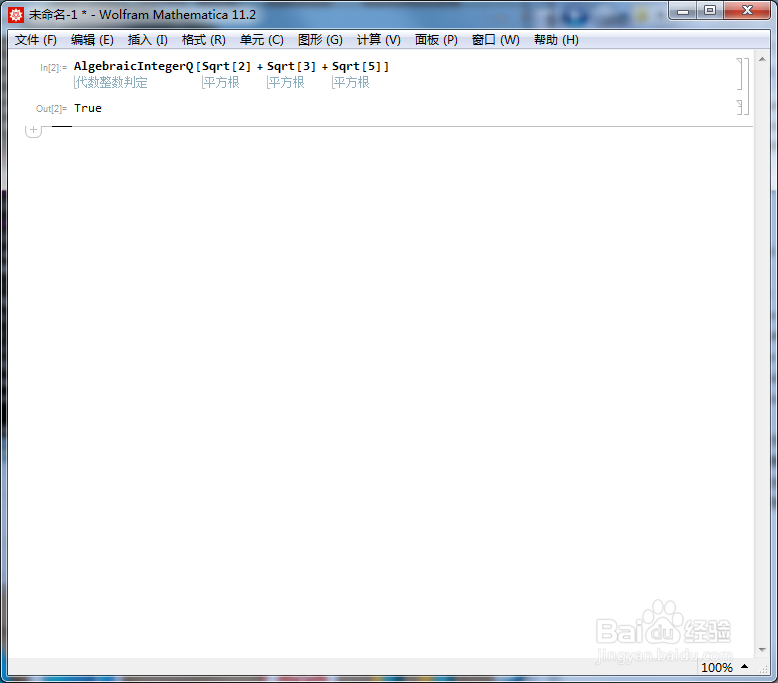 [图]3/6
[图]3/6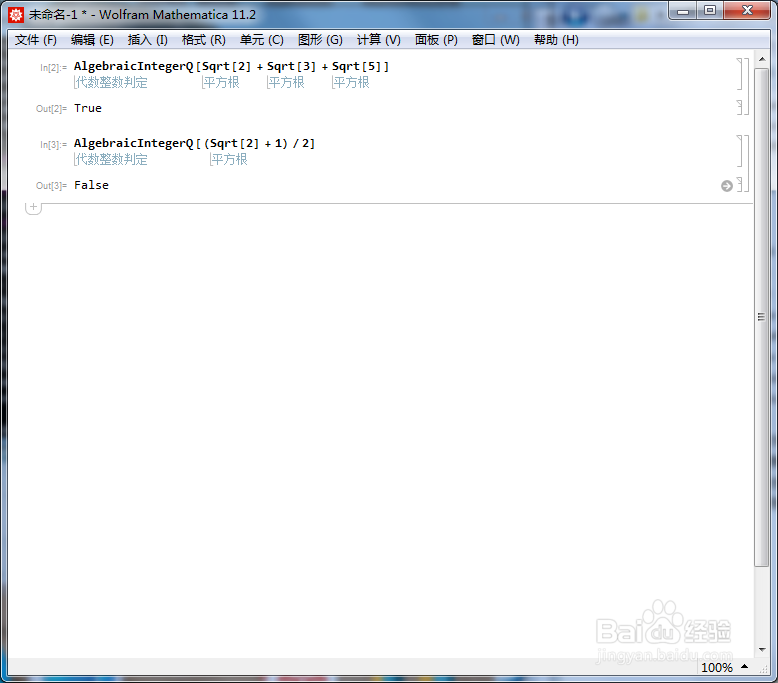 [图]4/6
[图]4/6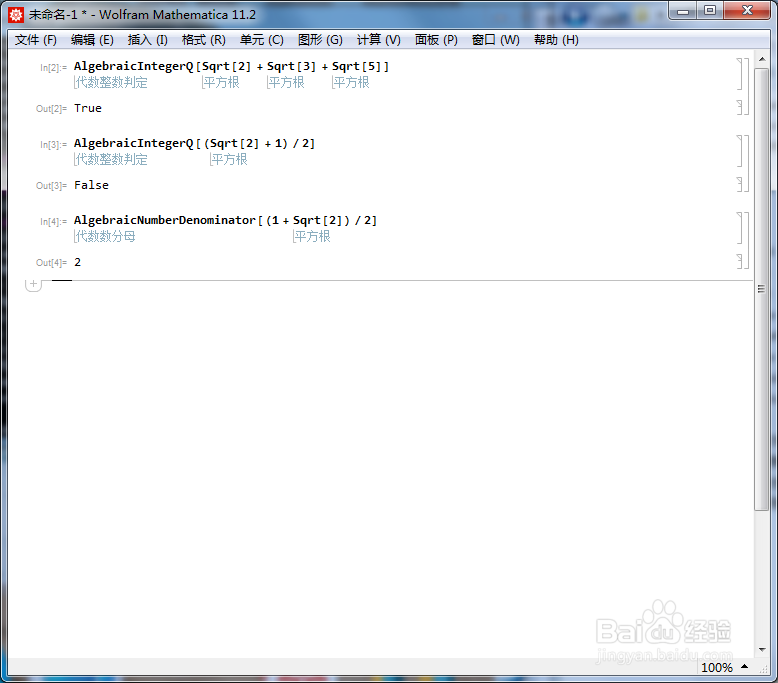 [图]5/6
[图]5/6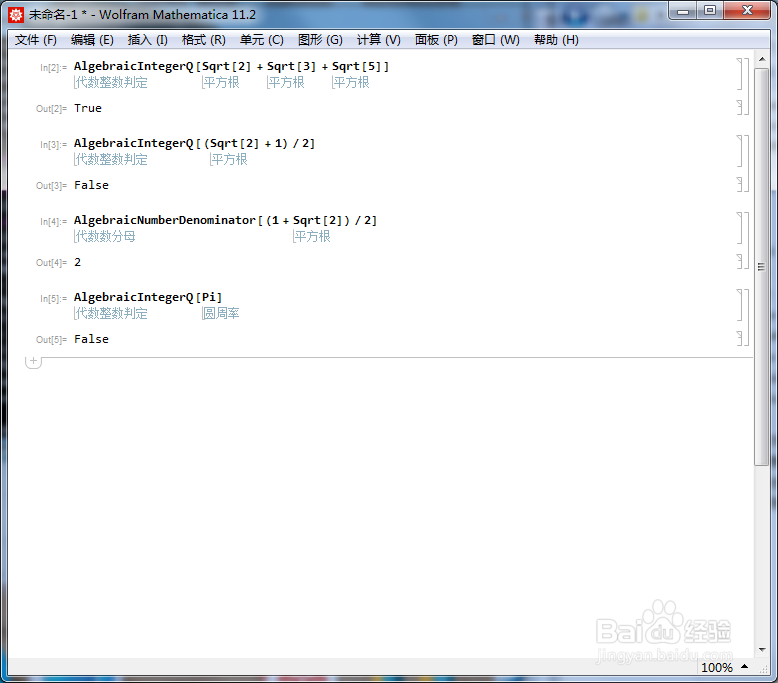 [图]6/6
[图]6/6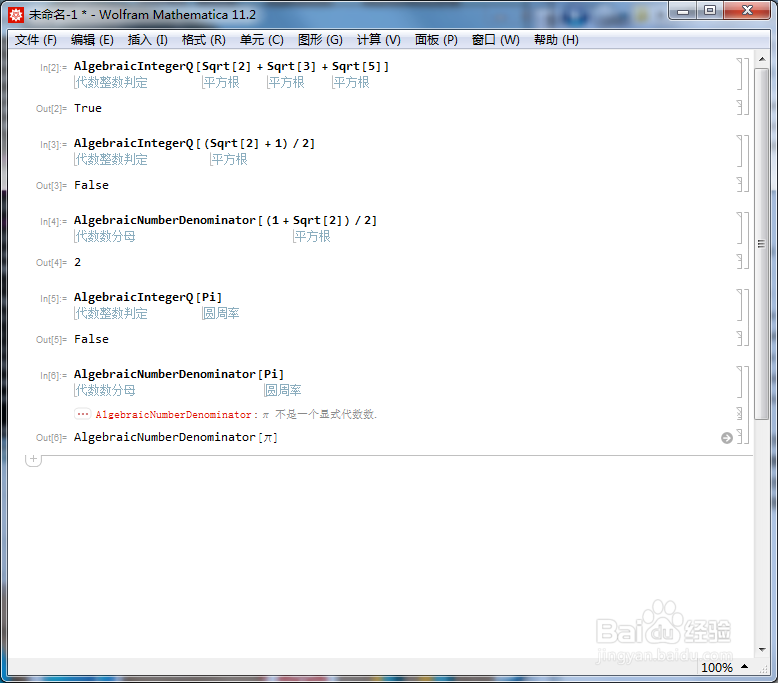 [图]
[图]
本文介绍的是,用Mathematica判断给定的数字是否代数数,以及是否代数整数的基本方法。
工具/原料
电脑Mathematica方法/步骤
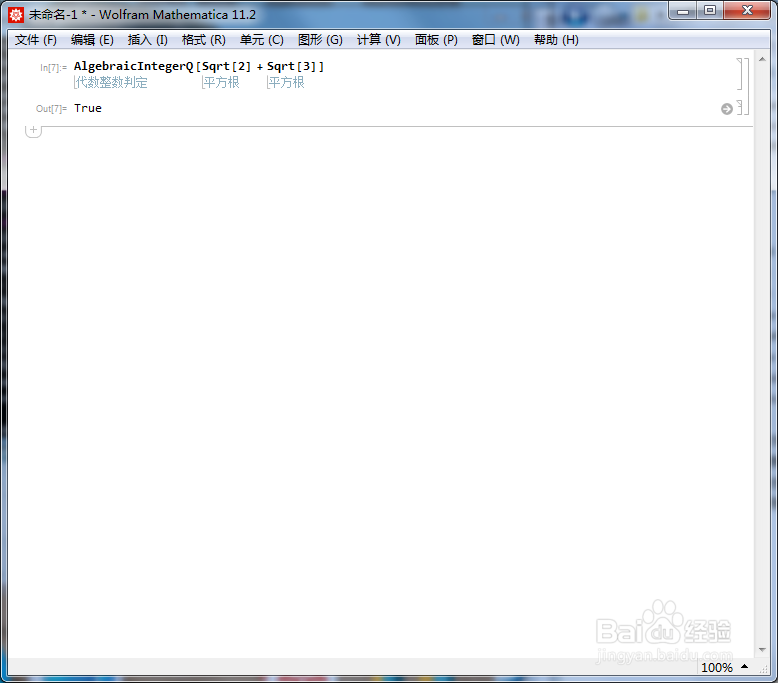
1/6分步阅读判断Sqrt[2] + Sqrt[3] 是不是代数整数的方法是:
AlgebraicIntegerQ[Sqrt[2] + Sqrt[3] ]
返回结果是True,则表示它是代数整数。
 [图]2/6
[图]2/6Sqrt[2] + Sqrt[3] + Sqrt[5]也是代数整数。
AlgebraicIntegerQ[Sqrt[2] + Sqrt[3] + Sqrt[5]]
 [图]3/6
[图]3/6(Sqrt[2] + 1)/2不是代数整数,所以返回的结果是False。
AlgebraicIntegerQ[(Sqrt[2] + 1)/2]
 [图]4/6
[图]4/6(Sqrt[2] + 1)/2乘上一个正整数n,使之变成一个代数整数,n最小是多少?
用下面的代码可以求出来:
AlgebraicNumberDenominator[(1 + Sqrt[2])/2]
 [图]5/6
[图]5/6圆周率π不是代数整数:
AlgebraicIntegerQ[Pi]
 [图]6/6
[图]6/6看看π要乘上一个多大的正整数,才能变成代数整数:
AlgebraicNumberDenominator[Pi]
结果报错,其根源是,π不是代数数。
 [图]
[图]编辑于2018-12-01,内容仅供参考并受版权保护
经验备注
我发现了这篇经验很有用:你也认同《【抽象代数】用Mathematica判定代数整数》的经验分享有价值,就请和朋友们一起分享吧。另外,【抽象代数】用Mathematica判定代数整数的经验内容仅供参考,如果您需解决具体问题(尤其法律、医学等领域),建议您详细咨询相关领域专业人士。经验知识实用生活指南-解决你所有的生活难题!未经许可,谢绝转载。本文网址:https://www.5058.cn/article/37bce2bebc5d761002f3a2b7.html
健康/养生经验推荐
- Q[视频]寻找手机自动关机怎么设置
- Q有多少如何徒手锻炼腹肌--每天8分钟科学专业...
- Q这里脸上长痘痘是什么原因
- Q都说蜂蜜水有哪些作用与功效
- Q优秀简单一招,帮你解酒护肝
- Q学习怎样可以长高,长高的科学方法
- Q哪个男女都适合!腹肌撕裂者分步骤详细图解
- Q我想日常生活怎么补肾
- Q有多少怎样才能让头发长的快
- Q我想14种鼻型图解
- Q怎么看痛经怎么办快速解决
- Q听说减肥最快的十种食物
- Q阐述怎样才能长高?
- Q这个指甲有竖纹的成因及治疗方法
- Q一般腰间盘突出的简单锻炼方法
- Q这里武术的基本功练习方法
- Q该不该低血压的原因及该怎么办
- Q你知道治疗颈椎病方法
- Q怎么做绝食(断食)减肥成功案例,10天爆瘦21...
- Q[视频]好不好蔬菜鸡蛋汉堡的做法
- Q天龙八部少室山副本攻略
- Q尼尔机械纪元 飞弹补给作战 任务攻略
- Q黑色羽绒服配什么颜色的毛衣好看?
已有 41684 位经验达人注册
已帮助 182258 人解决了问题


