[视频]【抽象代数】格和子格怎么用Mathematica绘制?
更新:2024-04-01 22:23:16优质经验
设矩阵a等于{{3, 1}, {-1, 2}},Z是整数环,V=Z^2,代表的是平面上的整点,还可以视为格。本文,就用Mathematica来绘制格V和它的子格a*V。
工具/原料
电脑Mathematica方法/步骤
1/6分步阅读我们先写一个自定义函数,用来根据给定的格基绘制相应的格。
f[w_, J_, color_, opacity_]
其中,w代表格子的某个顶点,J是由格基组成的矩阵,color代表格子的颜色,opacity代表透明度。
 [图]2/6
[图]2/6比如,Z^2的一个以原点为顶点的格子可以画为:
Show[f[{0, 0}, {{1, 0}, {0, 1}}, Green, 1], Axes -> True]
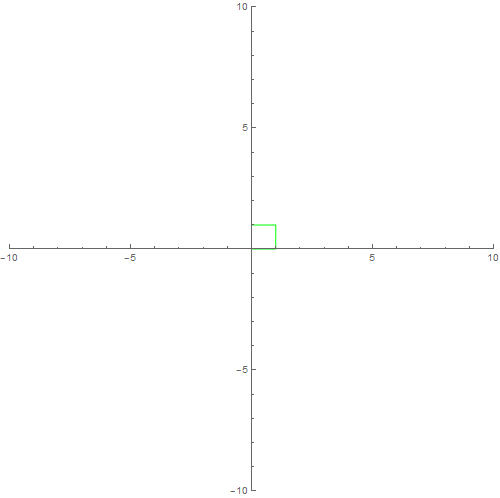 [图]3/6
[图]3/6我们当然可以把一定范围内所有的格子全部画出来:
A = Tuples[Range[-12, 11], 2];
Show[f[#, {{1, 0}, {0, 1}}, Green, 0.5] & /@ A,Axes -> True]
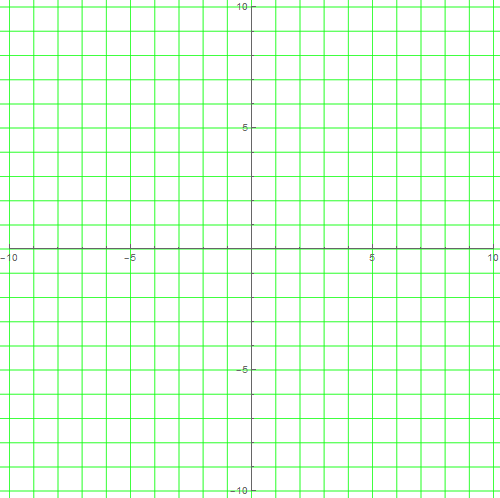 [图]4/6
[图]4/6用矩阵a左乘,会把格子变成别的形状:
a = {{3, 1}, {-1, 2}};
Show[
f[#, {{1, 0}, {0, 1}}, Green, 0.5] & /@ A,
f[{0, 0}, a, Blue, 1], Axes -> True]
a把一个绿色的小正方形变成了一个蓝色的平行四边形。
注意,这里直接把a当成了格子的基,因为a乘以2*2的单位矩阵,仍等于a。
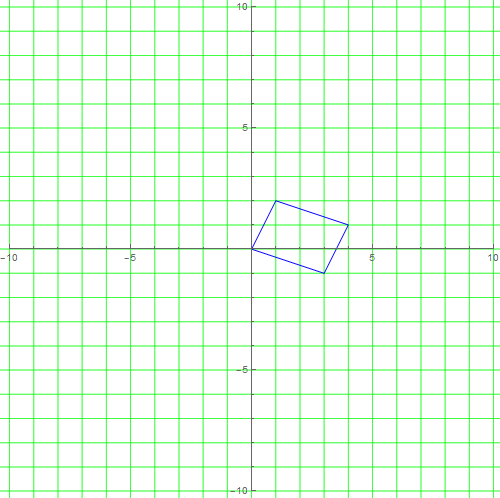 [图]5/6
[图]5/6我们也可以把附近所有的蓝色格子全部画出来:
Show[
f[#, {{1, 0}, {0, 1}}, Green, 0.5] & /@ A,
f[#, a, Blue, 1] & /@ (A.a\[Transpose]),
Axes -> True]
 [图]6/6
[图]6/6参考《【抽象代数】Z矩阵的对角化》里面的方法,可以把矩阵a简化为:
b={{1,0},{0,-7}};
那么我们可以画出b对应的格子:
Show[
f[#, {{1, 0}, {0, 1}}, Green, 0.5] & /@ A,
f[{0, 0}, b, Red, 1]]
这是一个长条形的格子,恰好是由7个1*1的格子组成。
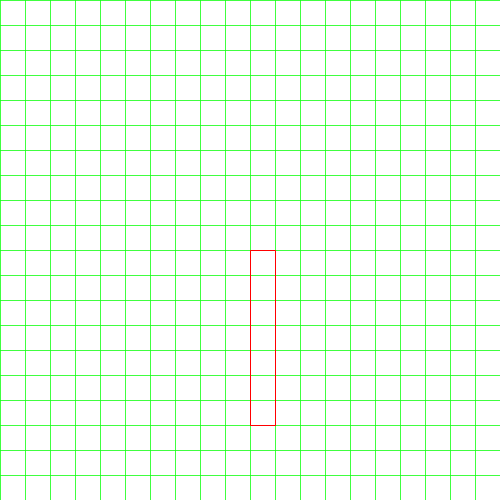 [图]
[图]时尚/美容经验推荐
- Q[视频]鲜芋牛奶糙米露的做法
- Q求大家怎样瘦腿才是最快方法
- Q学习朋友圈一条线是屏蔽了还是删除了
- Q在哪里学生瘦脸的最快方法
- Q为什么如何瘦肚子:怎样快速瘦肚子
- Q怎么讲瑜伽入门动作图片教程
- Q关注怎样让脸变白
- Q这里领带打结详解
- Q哪种正确的淡妆化妆步骤-怎样画淡妆
- Q这个中国护肤品十大品牌排行榜
- Q为什么说全球护肤品十大排名,买得起的大牌必须...
- Q帮忙淑女怎样扎出小清新发型
- Q为啥中国护肤品十大品牌排行榜
- Q经常牛仔阔腿裤搭配什么鞋
- Q为啥夏天穿内衣很热怎么办
- Q可以怎样快速瘦肚子
- Q有了解全球十大护肤品排行榜,十款性价比高的...
- Q哪有怎么瘦大腿和屁股
- Q有了解中学生怎样快速瘦腿
- Q[视频]怎么做手机字体大小怎么调
- Q腾讯视频夜间模式怎么开启
- Q[视频]抖音支付方式怎么改成微信
- Q钉钉怎么切换主企业
已有 47844 位经验达人注册
已帮助 149467 人解决了问题


