[视频]怎么用Mathematica验证共形变换的保角性质?
关于凯迪拉克sls赛威怎么用Mathematica验证共形变换的保角性质?,期待您的经验分享,希望你能感受到,我最真诚的谢意
!
更新:2024-02-02 18:07:15杰出经验
来自豆瓣网https://www.douban.com/的优秀用户无情天魔精致,于2017-07-28在生活百科知识平台总结分享了一篇关于“怎么用Mathematica验证共形变换的保角性质?刘翔”的经验,非常感谢无情天魔精致的辛苦付出,他总结的解决技巧方法及常用办法如下:
 [图]2/5
[图]2/5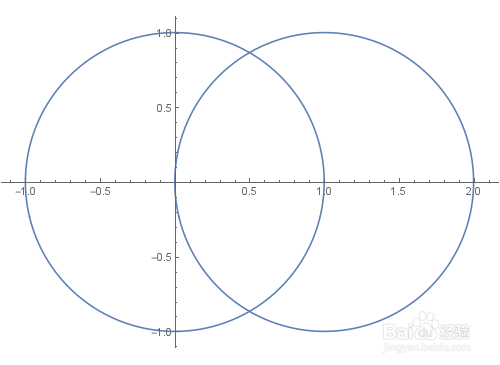 [图]
[图] [图]
[图] [图]3/5
[图]3/5 [图]4/5
[图]4/5 [图]5/5
[图]5/5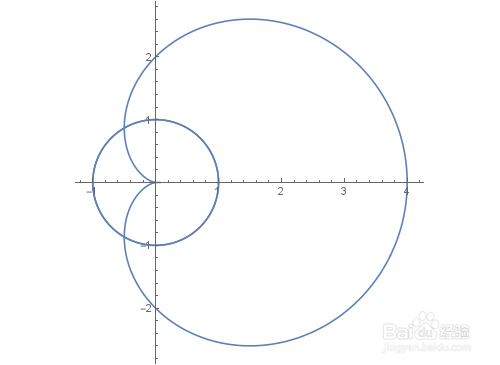 [图]
[图] [图]
[图] [图]
[图]
共形变换,保持图形微小区域的相似性,同时还有保角性质。下面,我们就用Mathematica来验证一下共形变换的保角性质。
工具/原料
电脑Mathematica方法/步骤
1/5分步阅读给出两个复数方程:
z0=Cos[t]+I Sin[t];z1=Cos[t]+1+I Sin[t];
 [图]2/5
[图]2/5作出z0和z1在复平面上对应的图像,代码是:
ParametricPlot[ReIm/@{z0,z1},{t,0,2 Pi}]
曲线z0和z1在交点处的夹角是:60°。
 [图]
[图] [图]
[图] [图]3/5
[图]3/5对z0和z1进行如下的共形变换:
f[x_]:=x^2
ParametricPlot[ReIm[f[x]],{x,-6 Pi,6 Pi}]
 [图]4/5
[图]4/5f作用于z0和z1,得到z2和z3,这是两个新的复数方程:
{z2,z3}=f/@{z0,z1}
 [图]5/5
[图]5/5在复平面上,作出z2和z3的图像:
ParametricPlot[ReIm/@{z2,z3},{t,0,2 Pi}]
z2和z3有两个实交点,还有两个复交点,这里只考虑实交点。
可以发现,曲线z2和z3在实交点处的夹角也是60°。
这就是共形变换的保角性质。
 [图]
[图] [图]
[图] [图]
[图]生活/家居经验推荐
- Q2022虎年纪念币怎么网上预约
- Q为什么说如何驯养柴犬
- Q有晓得微信如何能看到对方现在的位置?
- Q推荐怎么去电除水壶里的水垢
- Q那样如何快速去干枣核?
- Q什么情况怎么防止土豆发芽?
- Q如何选择宝妈如何做到工作与接孩子两不误?
- Q怎么讲如何让拖把不倒?
- Q这样iphone7正在搜索无服务如何处理
- Q哪儿如何正确的在鱼缸中种植水草
- Q有了解和女生聊天技巧,看了马上告别光棍。
- Q会不会知道车牌号怎么查询车主电话
- Q如何如何正确的跑步锻炼
- Q如何第一次坐飞机注意事项?
- Q要怎么怎样在网上预约办理离婚
- Q怎么打了狂犬疫苗后的注意事项
- Q有了解关于如何练字,分享给想练好书法的人
- Q优秀政府怎样知道你是否加入其他国籍?
- Q你知道豆芽的生长过程观察日记(7天左右带图解...
- Q[视频]微信收款码怎么隐藏真实姓名
- Q[视频]一般塞尔达打火石怎么获得
- Q阴阳师逐月之刻攻略
- Q王者抢先服怎么进入注册
已有 42871 位经验达人注册
已帮助 262313 人解决了问题


