[视频]【抽象代数】正四面体群的三维矩阵表示
关于急先锋【抽象代数】正四面体群的三维矩阵表示,期待您的经验分享,谢了,下次有事儿别忘了找我
!
更新:2024-03-29 15:02:11精品经验
来自爱奇艺https://www.iqiyi.com/的优秀用户无情天魔精致,于2018-11-16在生活百科知识平台总结分享了一篇关于“【抽象代数】正四面体群的三维矩阵表示羊驼”的经验,非常感谢无情天魔精致的辛苦付出,他总结的解决技巧方法及常用办法如下:
 [图]2/6
[图]2/6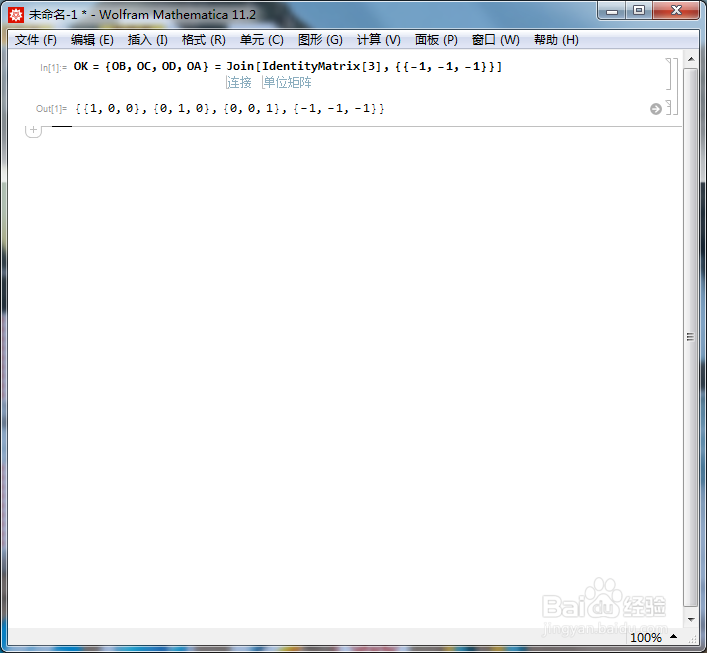 [图]3/6
[图]3/6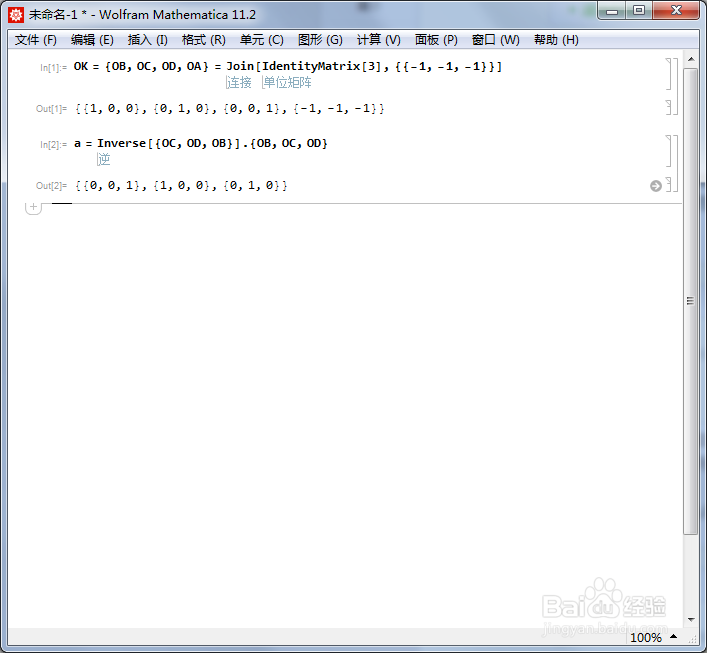 [图]4/6
[图]4/6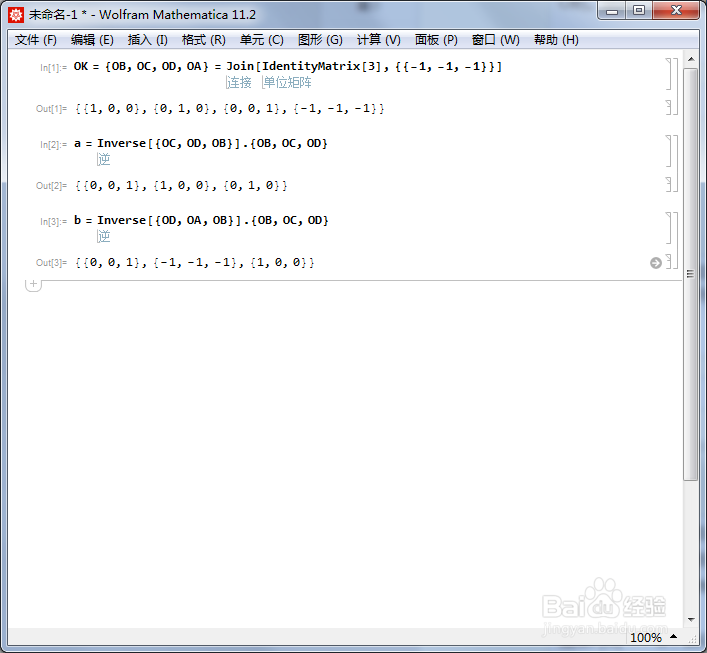 [图]5/6
[图]5/6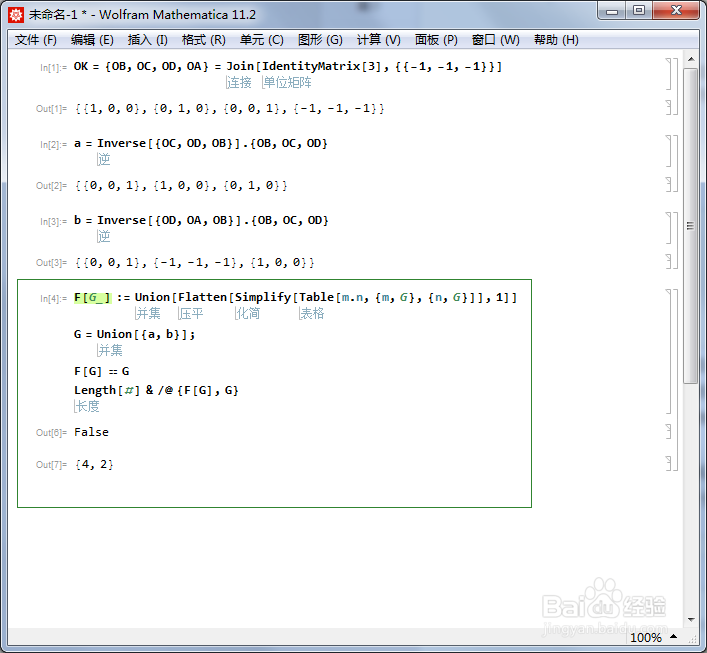 [图]6/6
[图]6/6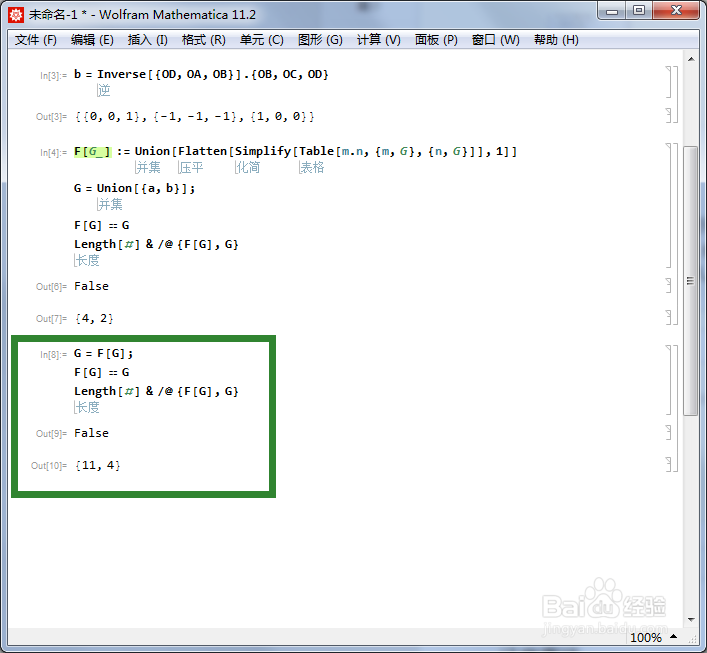 [图]
[图]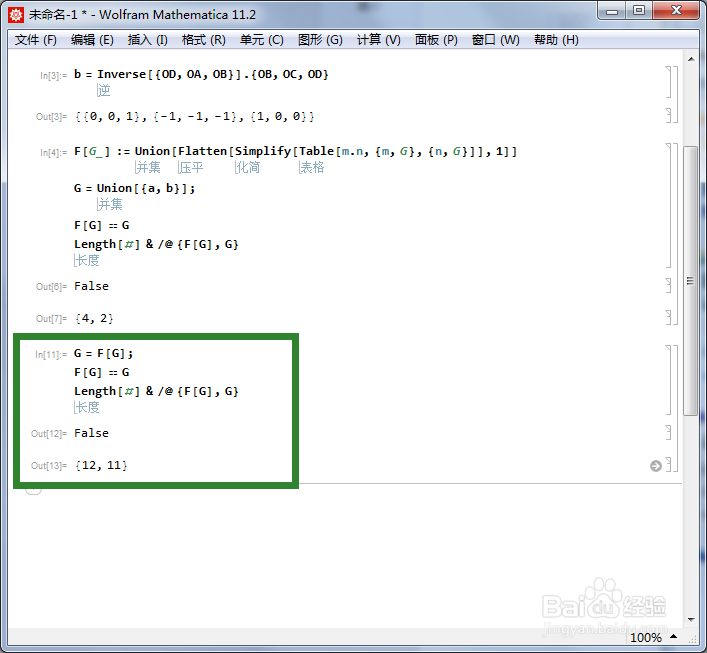 [图]
[图]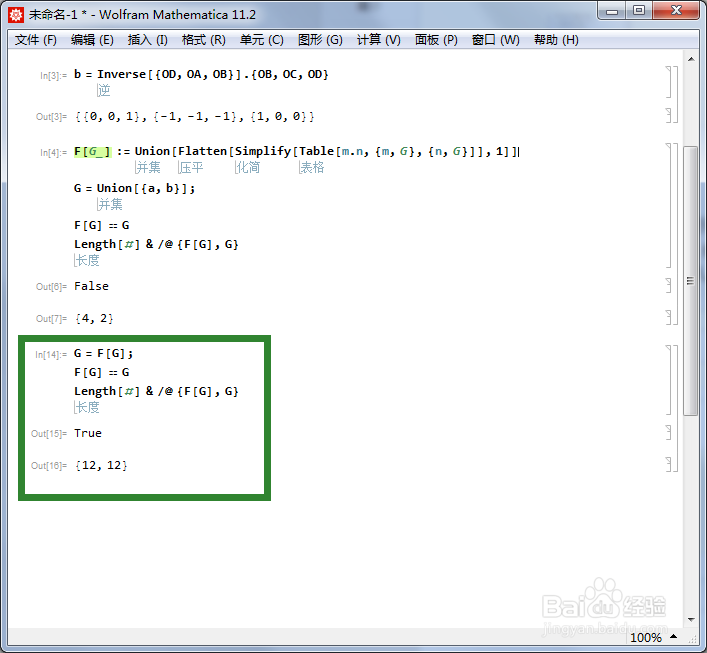 [图]
[图]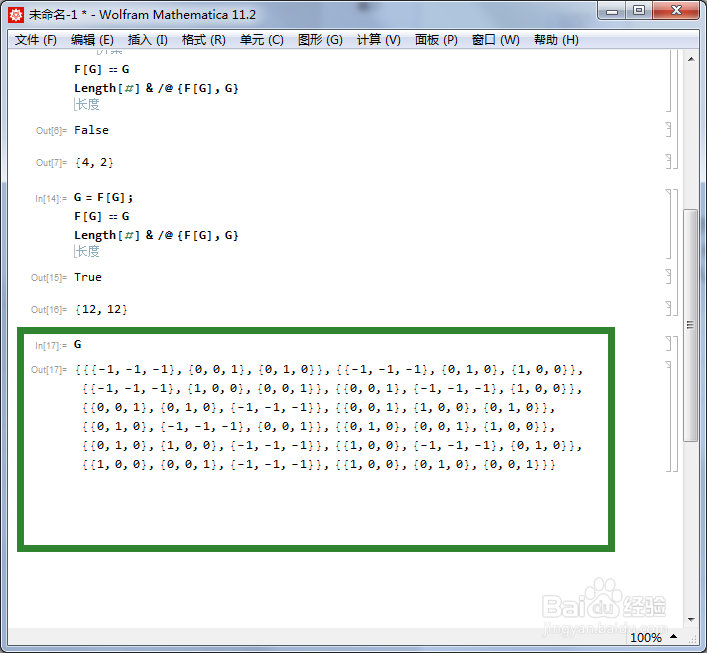 [图]
[图]
本文,介绍一下正四面体的对称群的三维表示。
工具/原料
电脑Mathematica方法/步骤
1/6分步阅读正四面体群最直接的表示,就是群元素作用于正四面体。
 [图]2/6
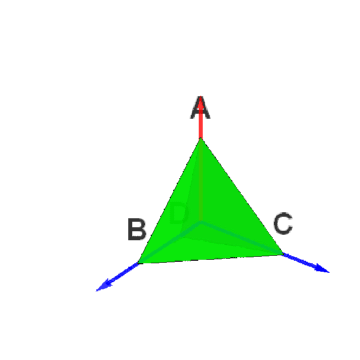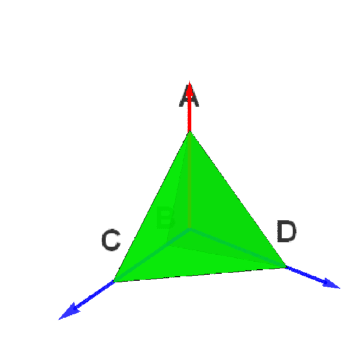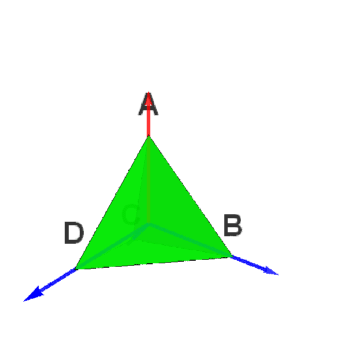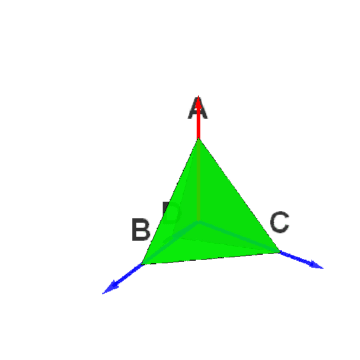
[图]2/6如果O为正四面体的中心,选择向量集合{OB、OC、OD}作为三维空间的基,那么,点B的坐标就可以写为:{1,0,0},点C的坐标就可以写为:{0,1,0},点D的坐标就可以写为:{0,0,1}。
进而,点A的坐标可以写为{-1,-1,-1},这是因为O=(A+B+C+D)/4。
 [图]3/6
[图]3/6以OA为旋转轴,旋转120°,这个变换记为a,它把{OB,OC,OD}变成了{OC,OD,OB}。因此,a对应的旋转矩阵可以表示为:
 [图]4/6
[图]4/6设AC的中点为X,BD的中点为Y,以XY为旋转轴旋转180°,把这个变换记为b,它把{OB,OC,OD}变成了{OD,OA,OB}。因此,b对应的旋转矩阵可以表示为:
 [图]5/6
[图]5/6这样,a和b就可以生成整个正四面体群。
先用集合{a,b}作乘法表,并查看乘法表里面的元素是否能够成为一个群:
F[G_] := Union[Flatten[Simplify[Table[m.n, {m, G}, {n, G}]], 1]]
G = Union[{a, b}];
如果F[G] == G,则G为群。
但是此时,F[G]四个元素,而G有两个元素,因此G不是群。
 [图]6/6
[图]6/6用F[G]代替G。
G = F[G];
F[G] == G
Length[#] & /@ {F[G], G}
这个程序运行三次,终于得到F[G] == G,此时G有12个元素。这恰好是正四面体群的一个三维表示。
 [图]
[图] [图]
[图] [图]
[图] [图]
[图]编辑于2018-11-16,内容仅供参考并受版权保护
经验备注
我发现了这篇经验很有用:你也认同《【抽象代数】正四面体群的三维矩阵表示》的经验分享有价值,就请和朋友们一起分享吧。另外,【抽象代数】正四面体群的三维矩阵表示的经验内容仅供参考,如果您需解决具体问题(尤其法律、医学等领域),建议您详细咨询相关领域专业人士。经验知识实用生活指南-解决你所有的生活难题!未经许可,谢绝转载。本文网址:https://www.5058.cn/article/af9f5a2d49728a43140a45da.html
美食/营养经验推荐
- Q如何开启小花生免打扰时间
- Q头条大蒜苗炒平菇
- Q用什么洋葱炒素鸡翅
- Q头条如何制作酸辣可口的油焖青椒
- Q怎么办鸡叉骨炖酸菜
- Q请告诉下洋葱炒白菜
- Q告诉洋葱炒海蛎
- Q回答下鸡叉骨炖白菜
- Q想知道鸡叉骨炖香菇
- Q为何鸡叉骨炖粉条
- Q一般平菇烧鸡叉骨
- Q好不好鸡脚眉豆木瓜汤
- Q这种酸辣包菜的做法
- Q哪些花生烧猪脚的做法
- Q求解答草莓酱的做法
- Q有啥红枣核桃糕备忘的做法
- Q怎么吃不腻的红烧肉的做法
- Q会不会小白系列:凉拌鸡胸肉的做法
- Q哪个香橙柠檬软欧的做法
- Q微信8.0.16更新了什么
- Q红米note10如何设置永不息屏?
- Q[视频]寻找手机自动关机怎么设置
- Q[视频]怎么写win+shift+s截图保存在哪
已有 39448 位经验达人注册
已帮助 287177 人解决了问题


