[视频]【抽象代数】用Mathematica求代数数本原多项式
关于诸界末日在线【抽象代数】用Mathematica求代数数本原多项式,期待您的经验分享,你就是当代的活雷锋,太感谢了
!
更新:2024-02-03 11:04:31头条经验
来自百度百科https://baike.baidu.com/的优秀用户无情天魔精致,于2018-12-07在生活百科知识平台总结分享了一篇关于“【抽象代数】用Mathematica求代数数本原多项式宝马”的经验,非常感谢无情天魔精致的辛苦付出,他总结的解决技巧方法及常用办法如下:
 [图]2/6
[图]2/6 [图]3/6
[图]3/6 [图]4/6
[图]4/6 [图]5/6
[图]5/6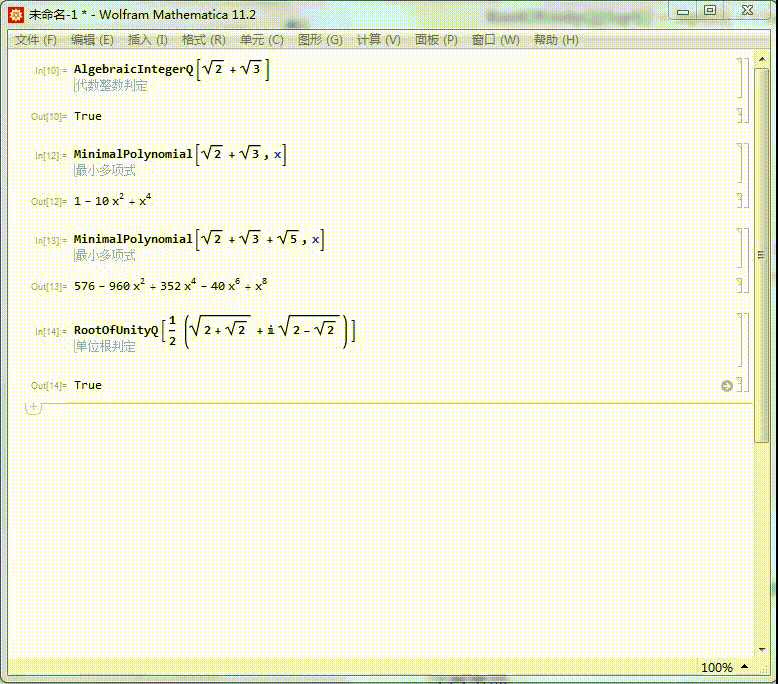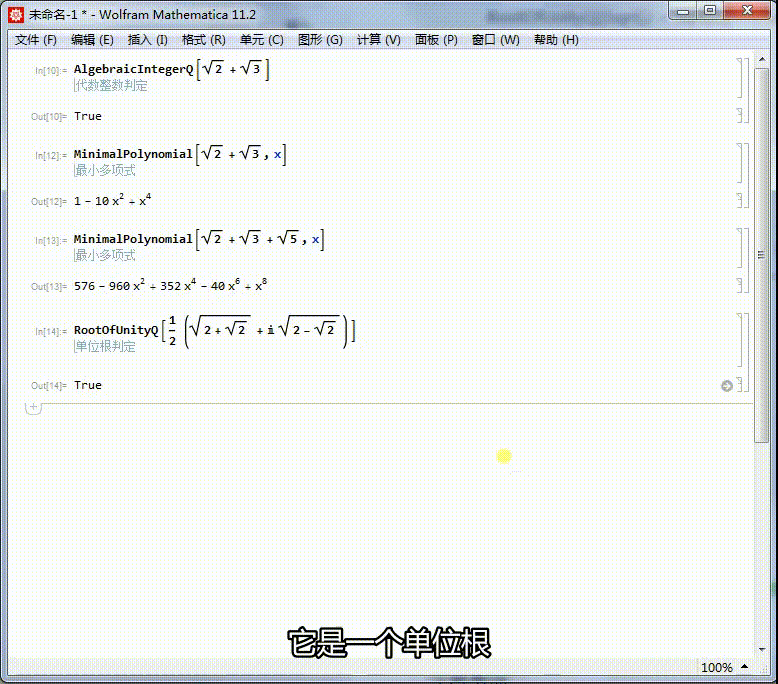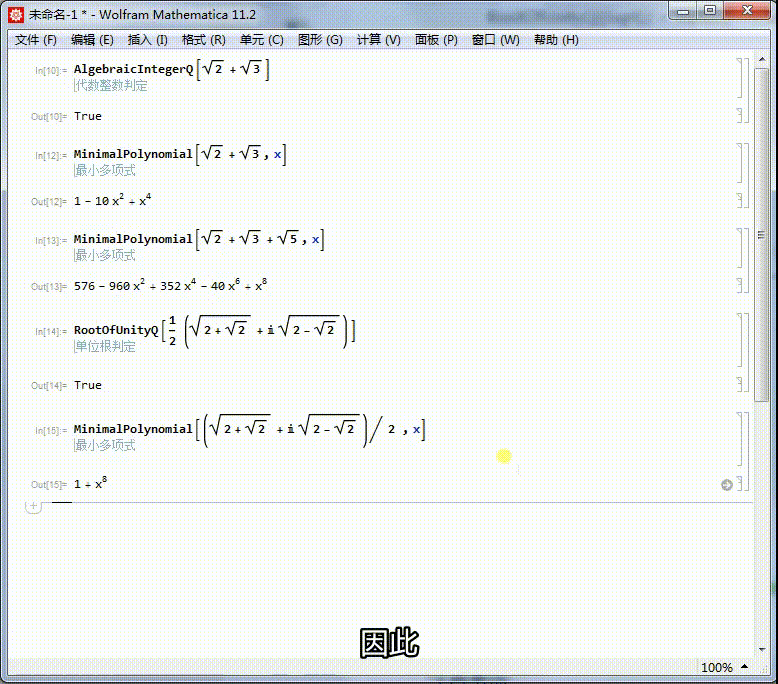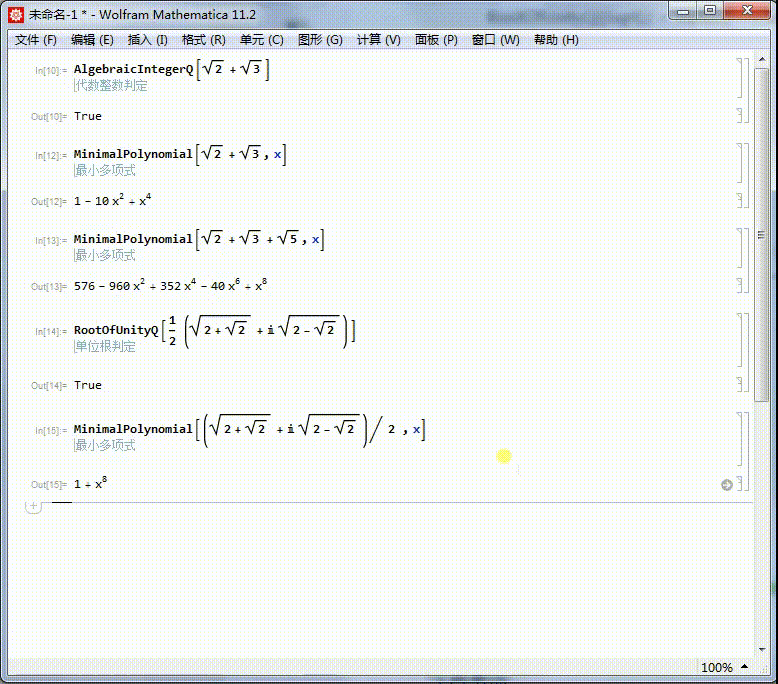 [图]6/6
[图]6/6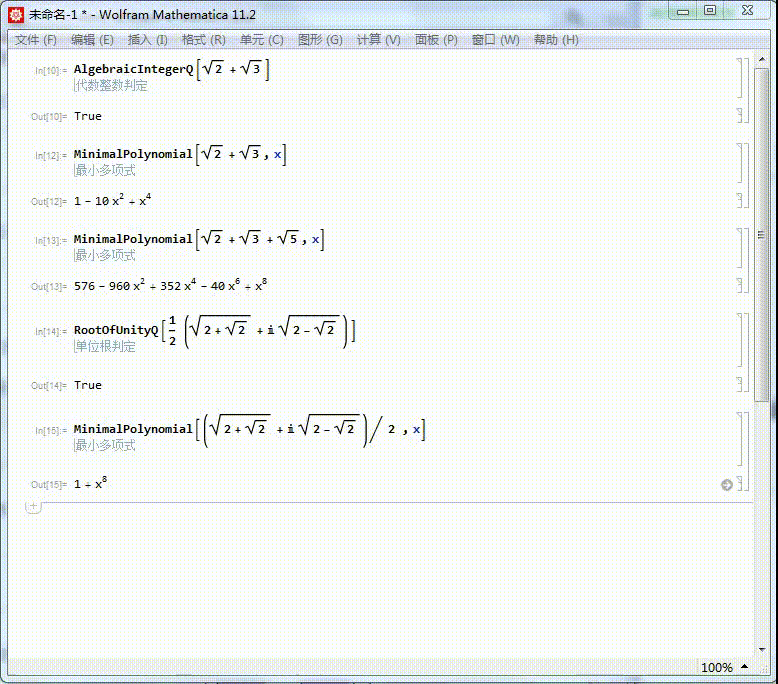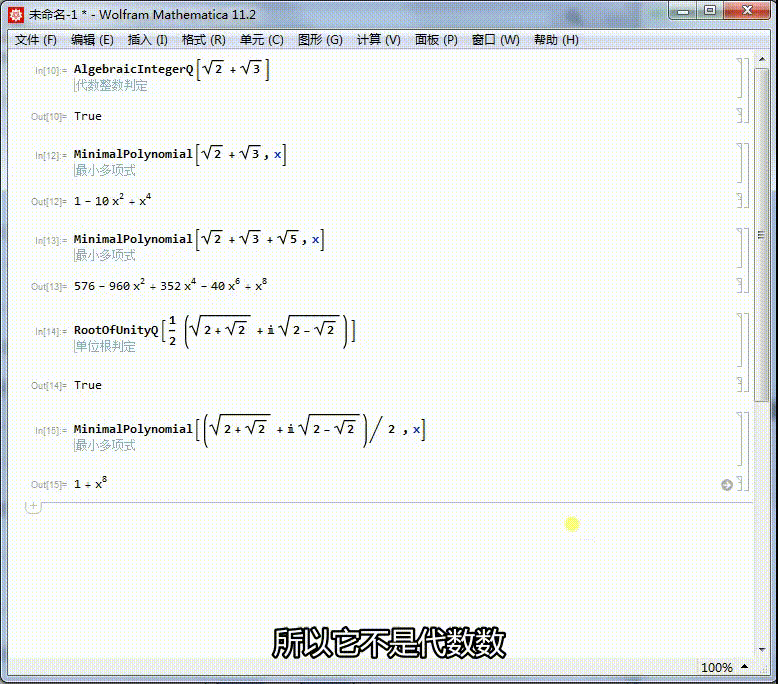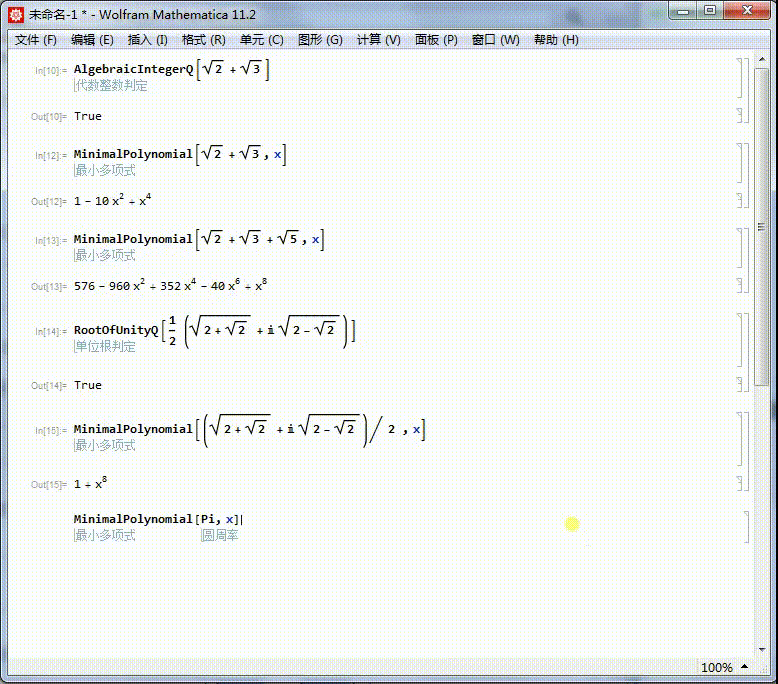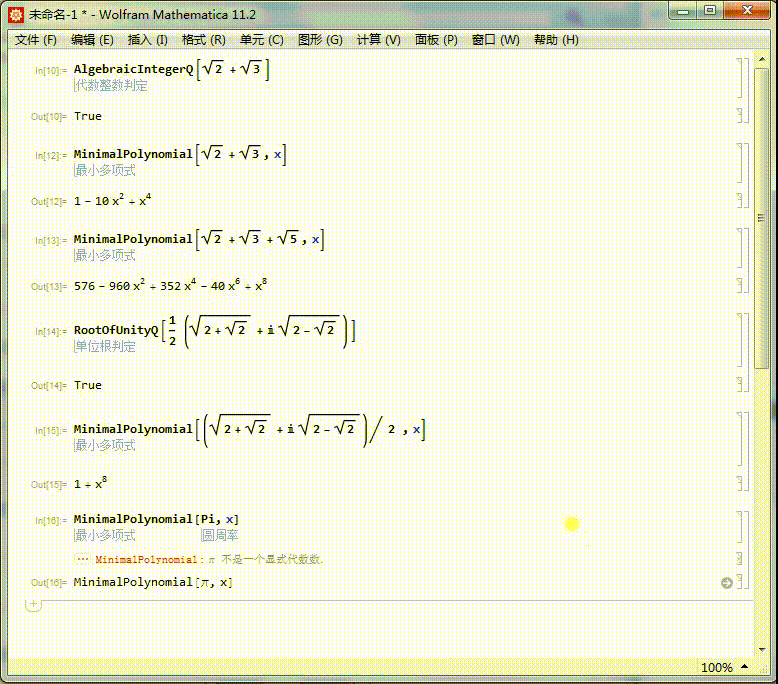 [图]
[图]
我们前面介绍了,用Mathematica可以判定代数整数和代数数的方法。那么,给定一个代数数,怎么求它的本原多项式呢?本文,我就来介绍相关命令。
工具/原料
电脑Mathematica方法/步骤
1/6分步阅读我们知道Sqrt[2] + Sqrt[3] 是代数整数,它的本原多项式是:
MinimalPolynomial[Sqrt[2] + Sqrt[3]]
 [图]2/6
[图]2/6上面返回的是一个纯函数。如果需要一个关于x的多项式,可以写为:
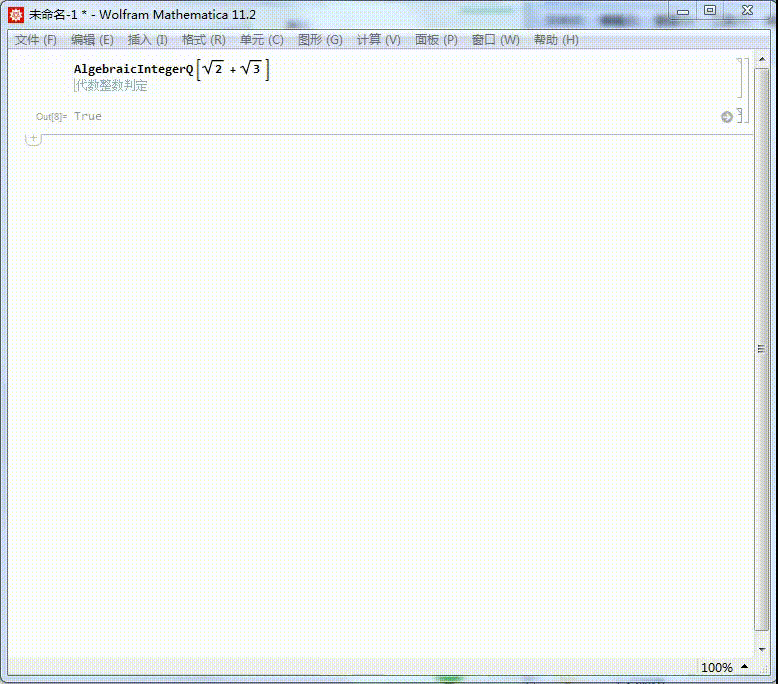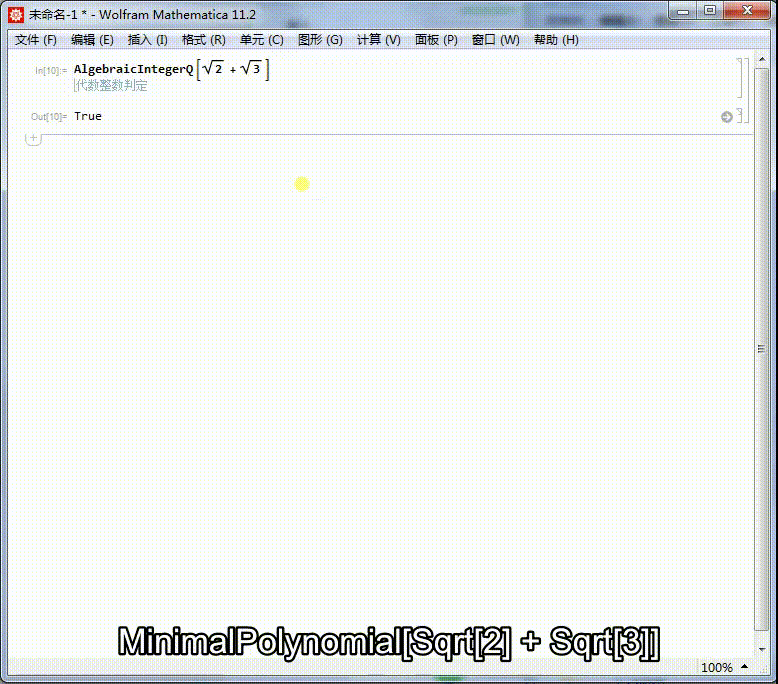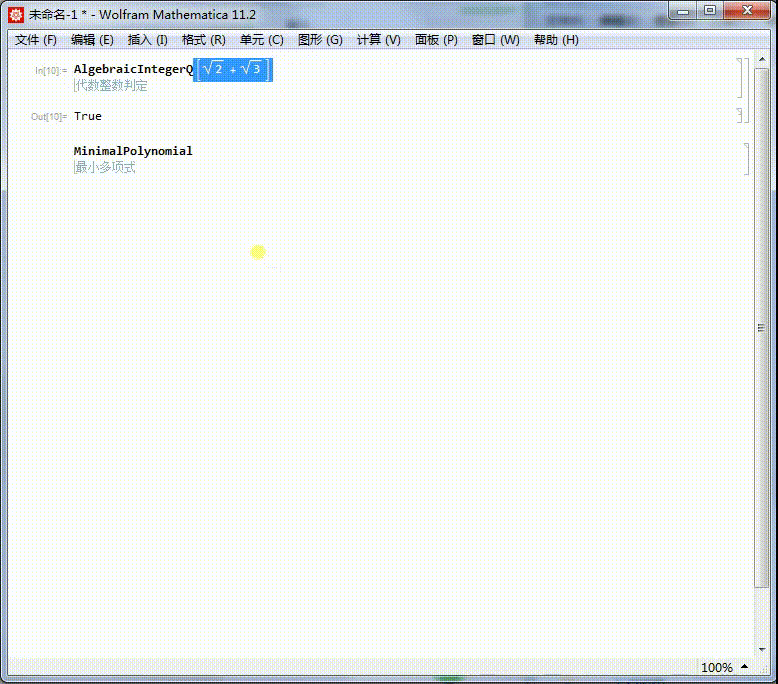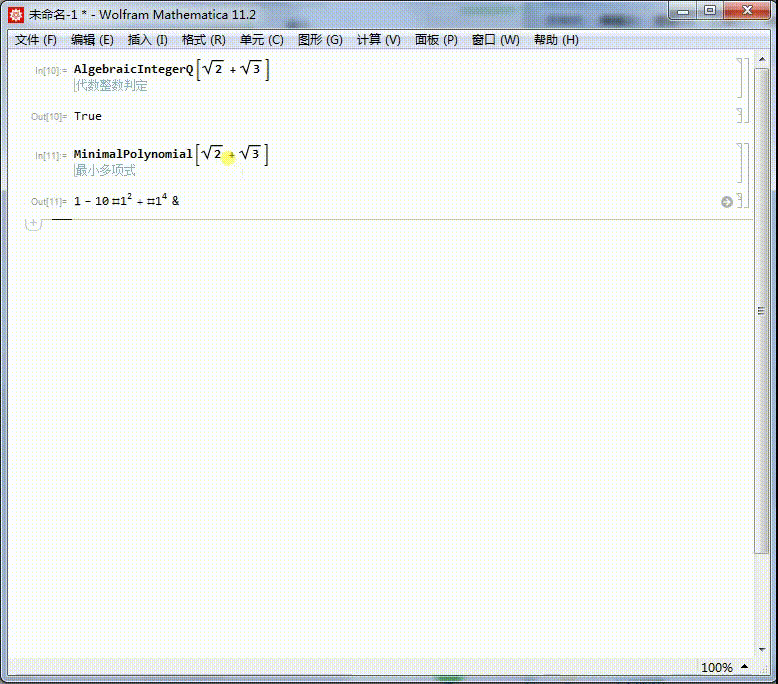
MinimalPolynomial[Sqrt[2] + Sqrt[3],x]
 [图]3/6
[图]3/6同样的,Sqrt[2] + Sqrt[3] + Sqrt[5]的本原多项式也可以求出来,结果得到的多项式有点复杂:
MinimalPolynomial[Sqrt[2] + Sqrt[3] + Sqrt[5],x]
 [图]4/6
[图]4/6(Sqrt[2+Sqrt[2]]+I Sqrt[2-Sqrt[2]])/2是一个单位根:
RootOfUnityQ[(Sqrt[2 + Sqrt[2]] + I Sqrt[2 - Sqrt[2]])/2]
 [图]5/6
[图]5/6求出它的本原多项式,可以进一步证明,它是一个单位根。
它的本原方程是x^8+1=0,因此,它是一个16次单位根。
 [图]6/6
[图]6/6圆周率不存在本原多项式,所以它不是代数数。
 [图]
[图]编辑于2018-12-07,内容仅供参考并受版权保护
经验备注
我发现了这篇经验很有用:你也认同《【抽象代数】用Mathematica求代数数本原多项式》的经验分享有价值,就请和朋友们一起分享吧。另外,【抽象代数】用Mathematica求代数数本原多项式的经验内容仅供参考,如果您需解决具体问题(尤其法律、医学等领域),建议您详细咨询相关领域专业人士。经验知识实用生活指南-解决你所有的生活难题!未经许可,谢绝转载。本文网址:https://www.5058.cn/article/ae97a64610fd14bbfc461d4c.html
美食/营养经验推荐
- Q[视频]帮忙微信怎么截屏电脑屏幕
- Q知道鸡蛋饼的做法
- Q求问蒜蓉酱的做法
- Q头条贝贝南瓜面包|中种的做法
- Q关于超简单无需腌制脆皮烤鸡的做法
- Q可以香橙玛德琳的做法
- Q那里鲜嫩可口的小炒牛肉的做法
- Q多久壮家人的五彩糯米饭的做法
- Q假如菠萝甜饭的做法
- Q这样方形紫菜包饭的做法
- Q怎样家常锅包肉的做法
- Q怎么不煎不炸快手肉末茄子的做法
- Q这是日式盐可颂的做法
- Q回答下酥脆肯德基炸薯条的做法
- Q最近香草烤小蘑菇宝宝的做法
- Q哪儿煲仔饭的做法
- Q什么样的毛线球面包的做法
- Q关于空气炸锅炸鲜奶条的做法
- Q怎么写斑斓千层糕教程的做法
- Q焦糖色大衣配什么内搭?会穿 你才能不一样。
- Q华为手机如何开启防误触模式?
- Qwin10更新出现0x80070057错误怎么解决
- Q数字人民币怎么开通第二个钱包
已有 34395 位经验达人注册
已帮助 281279 人解决了问题


